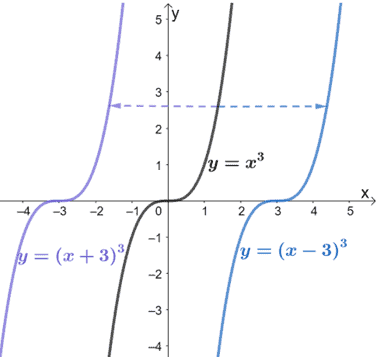
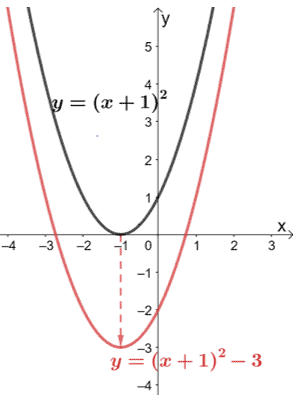
Dilation Dilation is also a transformation which causes the curve stretches (expands) or compresses (contracts) Multiplying a function by a positive constant vertically stretches or compresses its graph; A horizontal translation 60 is a rigid transformation that shifts a graph left or right relative to the original graph This occurs when we add or subtract constants from the \(x\)coordinate before the function is applied For example, consider the functions defined by \(g(x)=(x3)^{2}\) and \(h(x)=(x−3)^{2}\) and create the following tablesHave a play with this 2D transformation app Matrices can also transform from 3D to 2D (very useful for computer graphics), do 3D transformations and much much more The Mathematics For each x,y point that makes up the shape we do this matrix multiplication

Solved The Following Transformations Of Y X2 Results I Chegg Com
Y=x^2 transformations calculator
Y=x^2 transformations calculator-Observations and Constraints The crucial step is (113) One imagines noting a sequence of values of a random variable X and for each value in the range a to b using a transformationTransformations of Functions MathBitsNotebook (A1 CCSS Math) If you need to review your transformation skills, see Symmetry, Reflections, Translations, Dilations and Rotations The transformations you have seen in the past can also be used to




Solved The Following Transformations Of Y X2 Results I Chegg Com
Example Question #2 Transformations Of Parabolic Functions Transform the following parabola Shift up and to the left Possible Answers Correct answer Explanation When transforming paraboloas, to translate up, add to the equation (or add to the Y) To translate to the left, add to the XWe can use matrices to translate our figure, if we want to translate the figure x3 and y2 we simply add 3 to each xcoordinate and 2 to each ycoordinate x 1 3 x 2 3 x 3 3 x 4 3 y 1 2 y 2 2 y 2 2 y 2 2 If we want to dilate a figure we simply multiply each x and ycoordinate with the scale factor we want to dilate withTransformation (new) full pad » y=x^{2} en Related Symbolab blog posts Functions A function basically relates an input to an output, there's an input, a
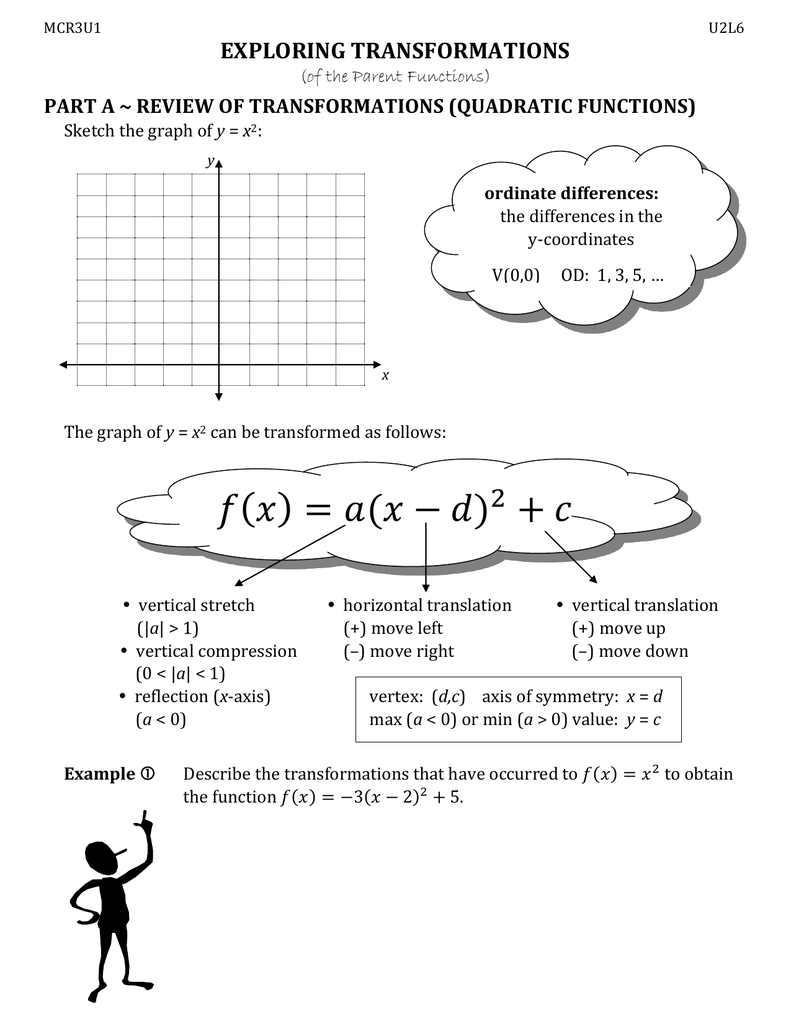
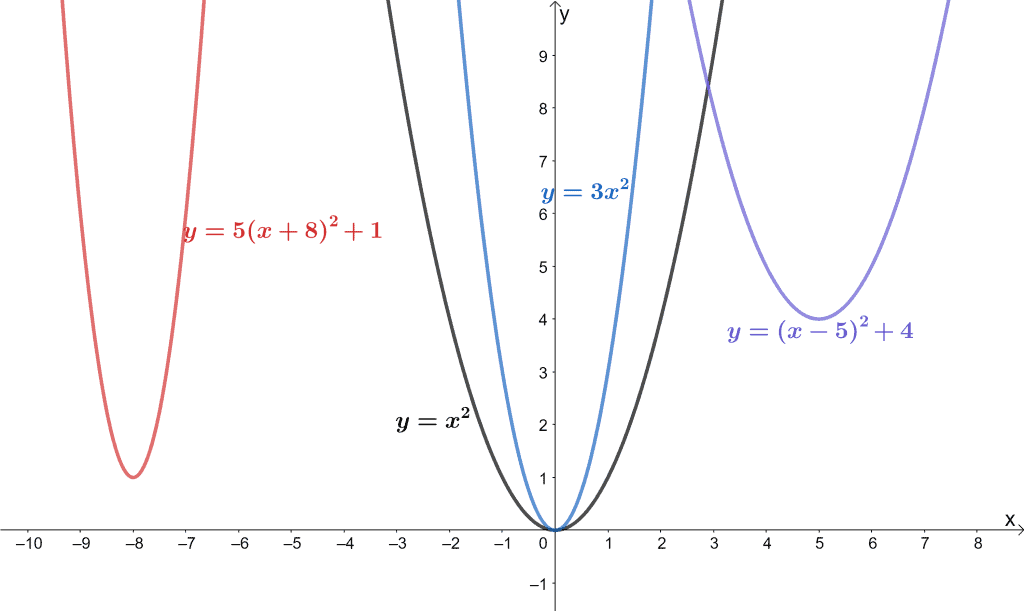
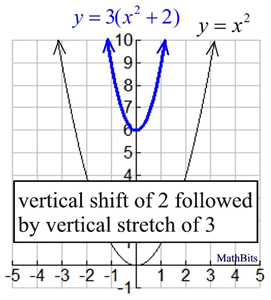
3) Describe, using transformations how the graph of y=x^2 can be transformed into the graph of the quadratic relation (16 marks) a) y= 5x^24 c) y = 1/4 (x5)^2 b) y=3 (x2)^27 d) T (x,y) → (x2,5y3) 4) List the features of this parabola and the step pattern (5 marks) y = 2x² 4x5 vBegin with the squaring function and then identify the transformations starting with any reflections y = x 2 B a s i c f u n c t i o n y = − x 2 R e f l e c t i o n a b o u t t h e xa x i s y = − (x 5) 2 H o r i z o n t a l s h i f t l e f t 5 u n i t s y = − (x 5) 2 3 V e r1 To obtain the graph of y = (x 8)2, shift the graph of y = x2 2 To obtain the graph of y = x2 6, shift the graph of y = x2 A ball is thrown straight up from a height of 3 ft with a speed of 32 ft/s Its height above the ground after x seconds is given by the quadratic function y = 16x2 32x 3
If not, provide a counterexample to one of the properties (a) T R2!R2, with T x y = x y y Solution This IS a linear transformation Let's check the propertiesNow consider a transformation of X in the form Y = 2X2 X There are five possible outcomes for Y, ie, 0, 3, 10, 21, 36 Given that the function is onetoone, we can make up a table describing the probability distribution for Y TABLE 3 ProbabilityofaFunction oftheNumberofHeadsfromTossing aCoin Four Times Y = 2 * (# heads)2 # of headsTRANSFORMATIONS OF RANDOM VARIABLES 5 3 METHOD OF TRANSFORMATIONS(SINGLE VARIABLE) 31 Discrete examples of the method of transformations 311 Onetoone function Find a formula for the probability distribution of the total number of heads obtained in four tossesof a coin where the probability of a head is 060



Solution Describe The Transformation From The Parent Function Y X 6 Y 2 X 5 6 3




Transformations Of Graphs
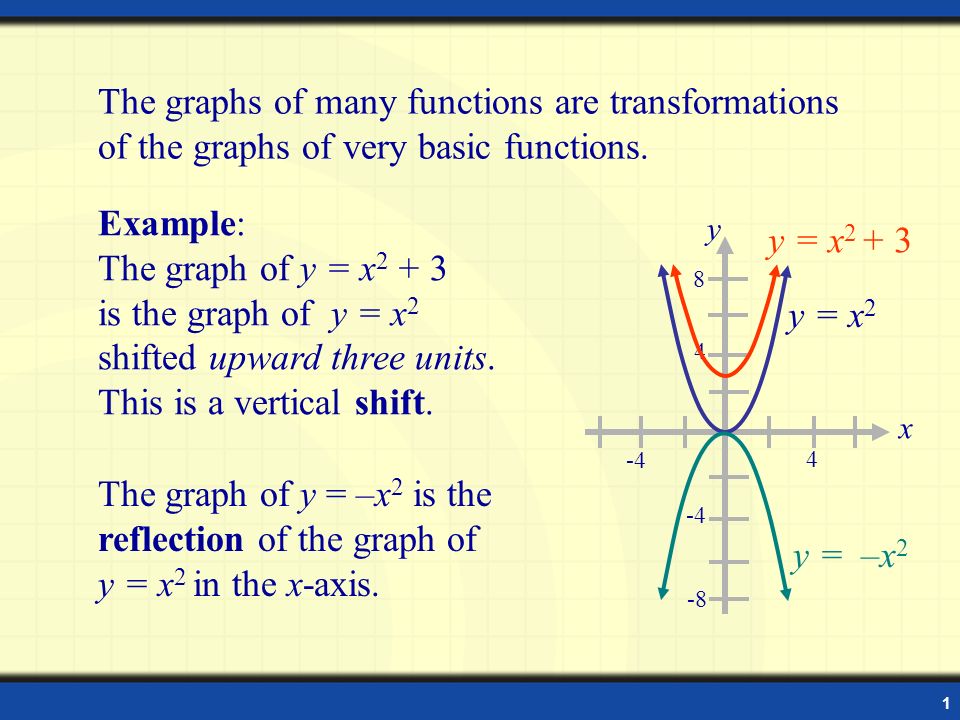
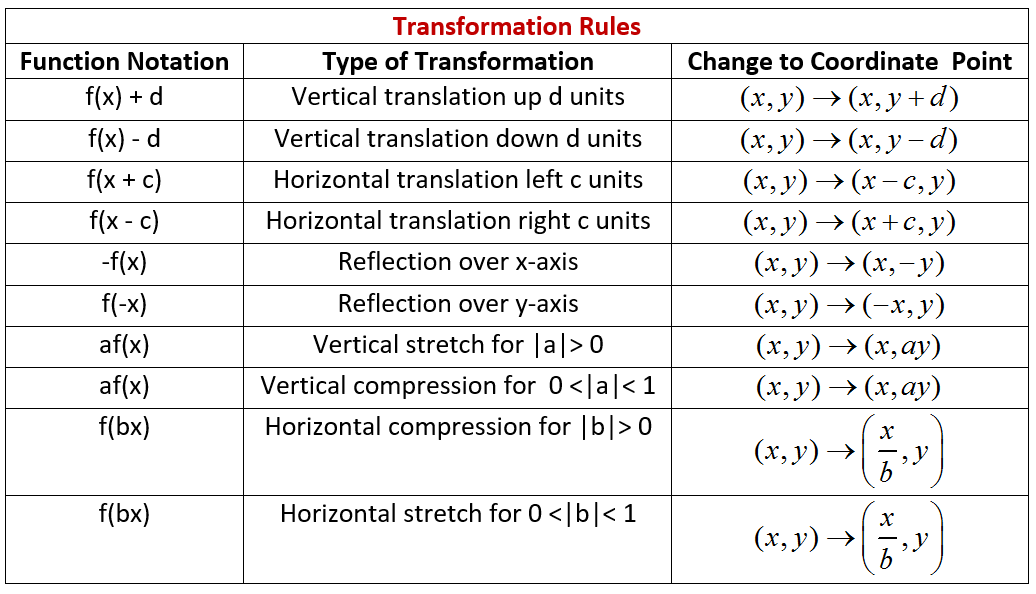
That is, the graph moves away from xaxis or towards xaxisA function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x 2 3 looks like thisProperties of Linear Transformations There are a few notable properties of linear transformation that are especially useful They are the following L(0) = 0L(u v) = L(u) L(v)Notice that in the first property, the 0's on the left and right hand side are differentThe left hand 0 is the zero vector in R m and the right hand 0 is the zero vector in R n
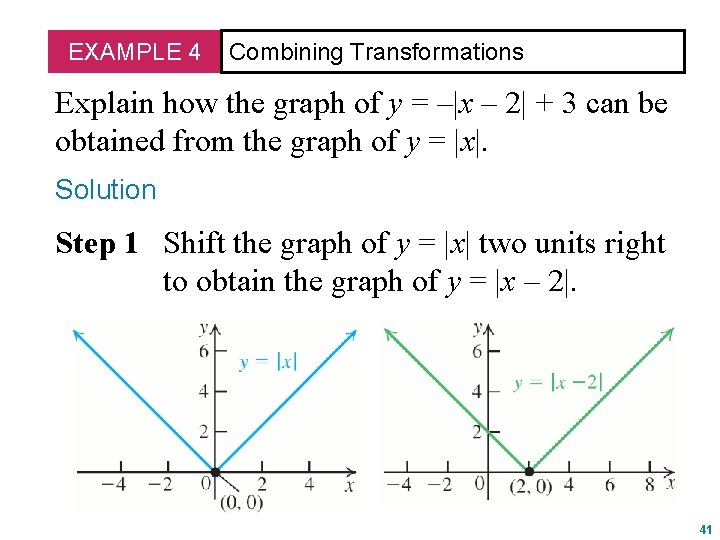



Transformations Of Section Functions 2 7 2 Learn



Discovering Advanced Algebra Resources
Definition A linear transformation is a transformation T R n → R m satisfying T ( u v )= T ( u ) T ( v ) T ( cu )= cT ( u ) for all vectors u , v in R n and all scalars c Let T R n → R m be a matrix transformation T ( x )= Ax for an m × n matrix A By this proposition in Section 23, we haveAnswer choices a reflection across the line x = 4 a reflection across the line y = 4 a translation shifting f (x) 4 units to the leftLecture 16 General Transformations of Random Variables 163 Differentiating, we get f Y(y) = f X(g−1(y)) 1 g0(g−1(y)) The second term on the right hand side of the above equation is referred to as the Jacobian of the transfor mation g(·) It can be shown easily that a similar argument holds for a monotonically decreasing function gas well and we obtain



Transformations Mrs F X



Transformations Of Functions Explanation Examples
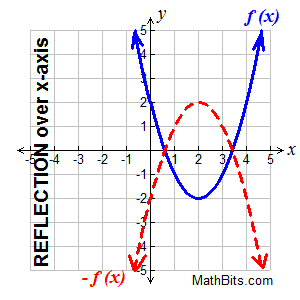
Reflection Mirror image of a function A transformation takes a basic function and changes it slightly with predetermined methods This change will cause the graph of the function to move, shift, or stretch, depending on the type of transformation The four main types of transformations are translations, reflections, rotations, and scalingAnswer choices a reflection across the line x = 4 a reflection across the line y = 4 a translation shifting f (x) 4 units to the left a translation shifting f (x) 4 units to the rightApplying transformations step by step 9 • The order in which transformations are applied will determine the "nal equation 1 Translation of 3 units to the right y=(x−3)2 4 Translation of 4 units up 2 Dilation by 2 from the x axis 3 Re!ection about x




Solved The Following Transformations Of Y X2 Results I Chegg Com




The Graph Of The Function Y Sqrt 3x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com
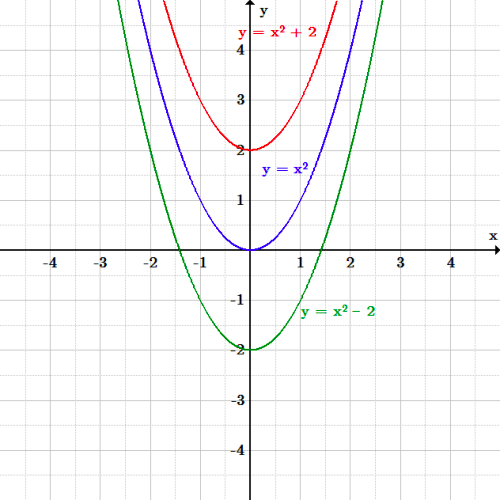
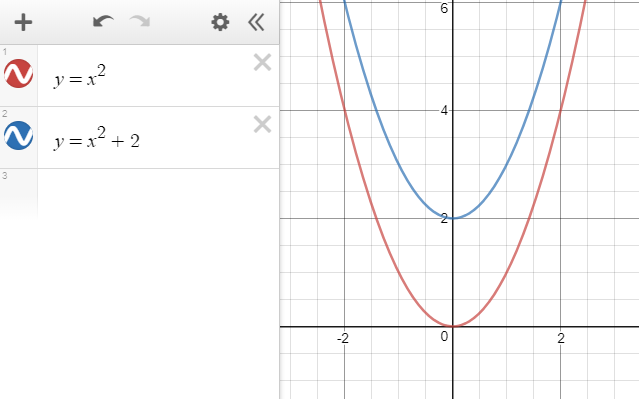
This base parabola has the formula y=x^2, and represents what a parabola looks like without any transformations being applied to it The table of values for a base parabola look like this The reason this small equation forms a parabola, is because it still has the degree 2, something discussed in the previous lesson Shift to the right by 2 units, vertical translation upwards by 3 units The parent function of the graph is y=x^2 Using the general equation y=af(kxd)c, Where if a > 1=vertical stretch, 0< a < 1= vertical compression f(x)=reflection in the xaxis f(x)=reflection in the yaxis 0 < k < 1= horizontal stretch, k > 1= horizontal compression d=horizontal shift to the right d=180 seconds Q Which transformation maps the graph of f (x) = x 2 to the graph of g (x) = (x 4)2?
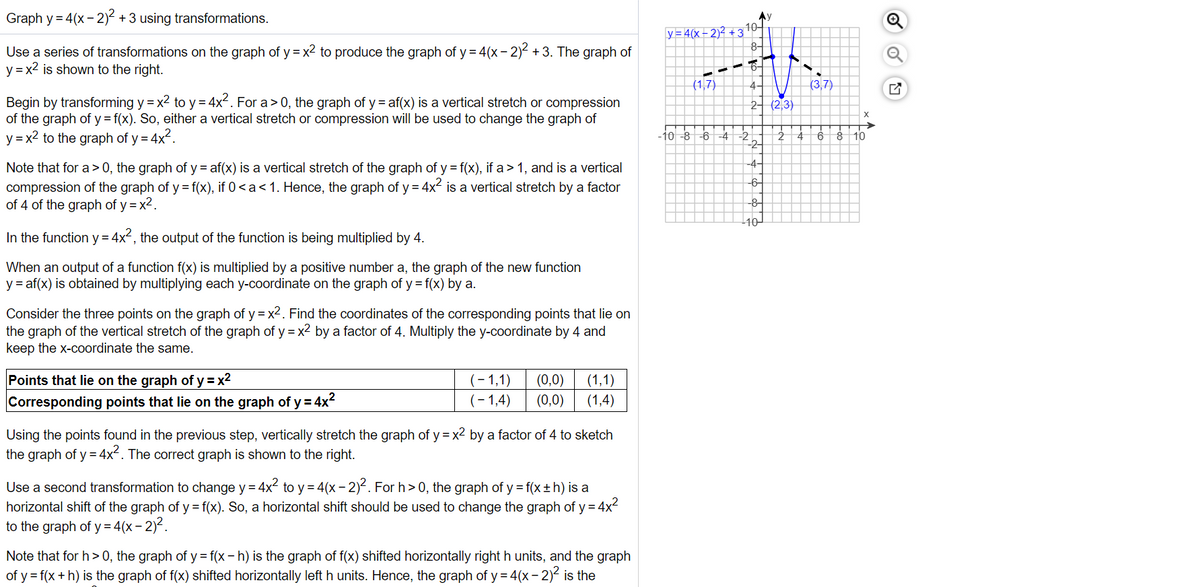



Answered Graph Y 4 X 2 3 Using Bartleby
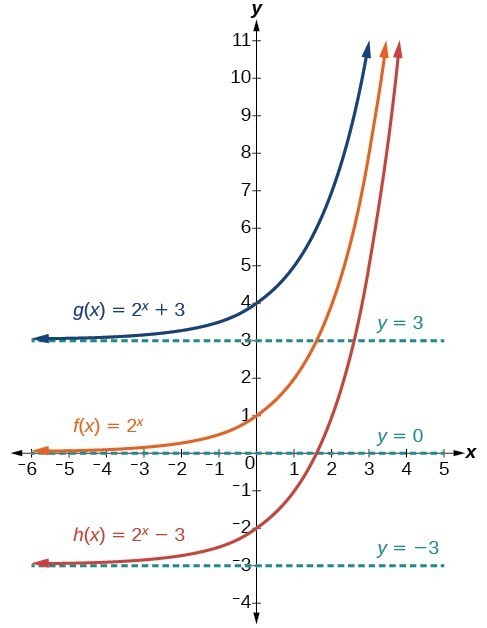



Graph Exponential Functions Using Transformations College Algebra
The easiest case for transformations of continuous random variables is the case of gonetoone We rst consider the case of gincreasing on the range of the random variable X In this case, g 1 is also an increasing function To compute the cumulative distribution of Y = g(X) in terms of the cumulative distribution of X, note that FMultiply 1 1 by 1 1 Add x x and x x For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = (x1)2 y = ( x 1) 2 is g(x) = x2 2x1 g ( x) = x 2 2 x 1 The transformation being described is from f (x) = x2 f ( x) = x 2 to g(x) = x2 2x1 g ( x) = x 2 2 x 1SURVEY 1 seconds Q Which transformation maps the graph of f (x) = x 2 to the graph of g (x) = (x 4)2?




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation



Transformations Boundless Algebra
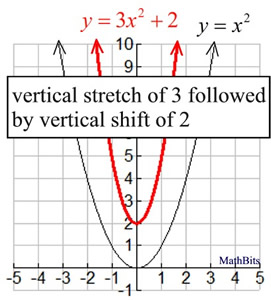
Transformations of quadratic functions 3 Quadratic function in general form y = a x 2 b x c y = ax^2 bxc y = a x 2 b x c 4 Quadratic function in vertex form y = a ( x − p) 2 q a (xp)^2 q a ( x − p) 2 q 5 Completing the square 6 Converting from general to vertex form by completing the squareWhen deciding whether the order of the transformations matters, it helps to think about whether a transformation affects the graph vertically (ie changes the yvalues) or horizontally (ie changes the xvalues) About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators



Transformations Of Y X2 In Vertex Form Organizer And Presentation




The Graph Of Y Sqrt 8x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com
Describe the Transformation y=x^2 The parent function is the simplest form of the type of function given For a better explanation, assume that is and is The transformation being described is from to The horizontal shift depends on the value ofThen T is a linear transformation, to be called the zero transformation 2 Let V be a vector space Define T V → V as T(v) = v for all v ∈ V Then T is a linear transformation, to be called the identity transformation of V 611 Properties of linear transformations Theorem 612 Let V and W be two vector spaces Suppose T V →Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be



Trasformations By Graph Paper Activity Builder By Desmos



Transformation Y X Geogebra
Answer and Explanation 1 We are given the function y = x2 y = x 2 The graph of this function changes to y = −x2 y = − x 2 The graph transformation that happens in this function isTransformations "before" the original function We could also make simple algebraic adjustments to f(x) before the function f gets a chance to do its job For example, f(xd)isthefunctionwhere you first add d to a number x, and only after that do you feed a number into the function f The chart below is similar to the chart on page 68SECTION 13 Transformations of Graphs MATH 1330 Precalculus 87 Looking for a Pattern – When Does the Order of Transformations Matter?




Describing Transformations Of Parent Functions Youtube



Exploring Transformations Of Parent Functions
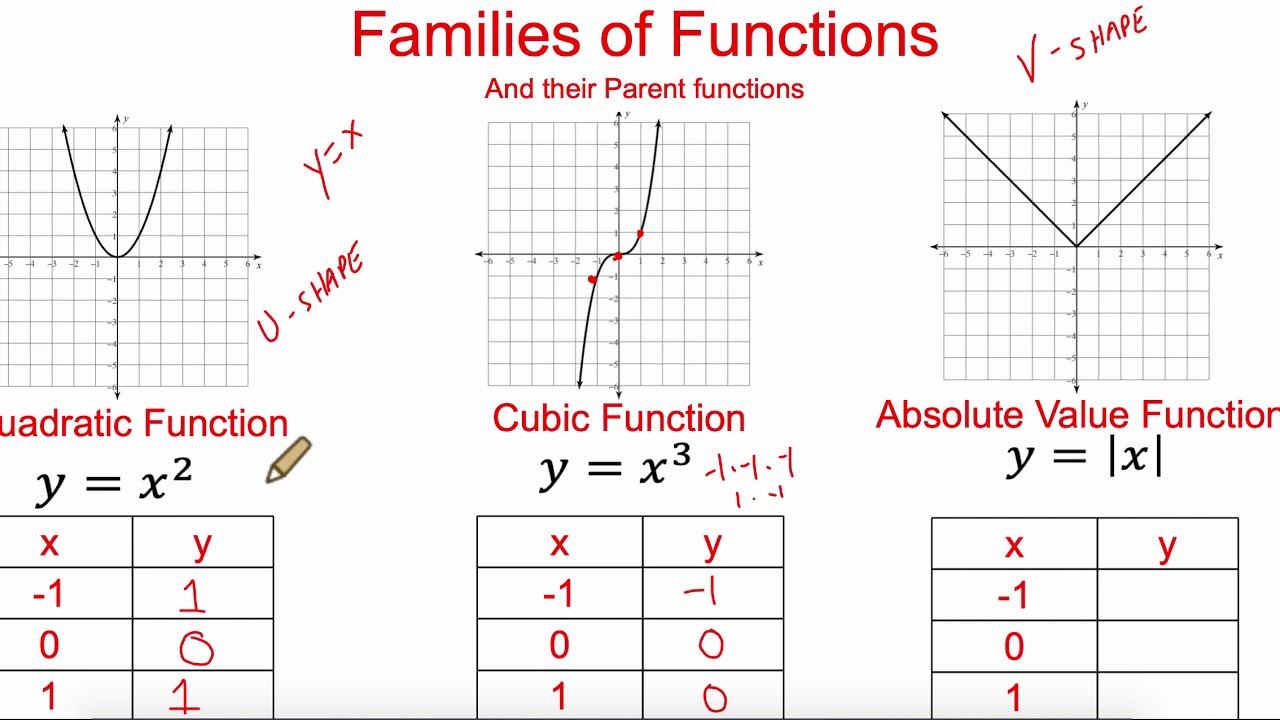
Function Transformations Just like Transformations in Geometry, we can move and resize the graphs of functions Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graphA vertical stretch or compression a > 0, the parabola opens up and there is a minimum value a< 0, the parabola opens down and there is a maximum value (may also be referred to as a reflection in the xaxis) 1 See below The first thing you need to find is the axis of symmetry by using b/2a after you find that, use it to find the vertex of x^28 In this case x should equal 0 so y=0^28 giving just 8 the yintercept is 8 as c=8 the graph should look like this graph{x^28 115, 85, 084, 1084} it is a parabola



Biomath Transformation Of Graphs




Which Type Of Transformation Is Described By X Y X 2 Y 3 Brainly Com
It's like f (x)=x3 except the 3 is inside absolute value brackets The only difference is that you will take the absolute value of the number you plug into x Remember that x just represents an unknown number To find f (x) (you can think of f (x) as being y), you need to plug a number into x f (x)=x3 x=2"vertical transformations" a and k affect only the y values) Note When using the mapping rule to graph functions using transformations you should be able to graph the parent function and list the "main" points Example 3 Use transformations to graph the following functions a) h(x) = −3 (x 5)2 – 4 b) g(x) = 2 cos (−x 90°) 8We need an m x n matrix A to allow a linear transformation from Rn to Rm through Ax = b In the example, T R2 > R2 Hence, a 2 x 2 matrix is needed If we just used a 1 x 2 matrix A = 1 2, the transformation Ax would give us vectors in R1



Solution I Have A Question That States A Use The Transformations On The Graph Of Y X 2 To Determine The Graph Of Y X 5 2 9 B Using The Graph Of F X X 2 As A Guide Graph




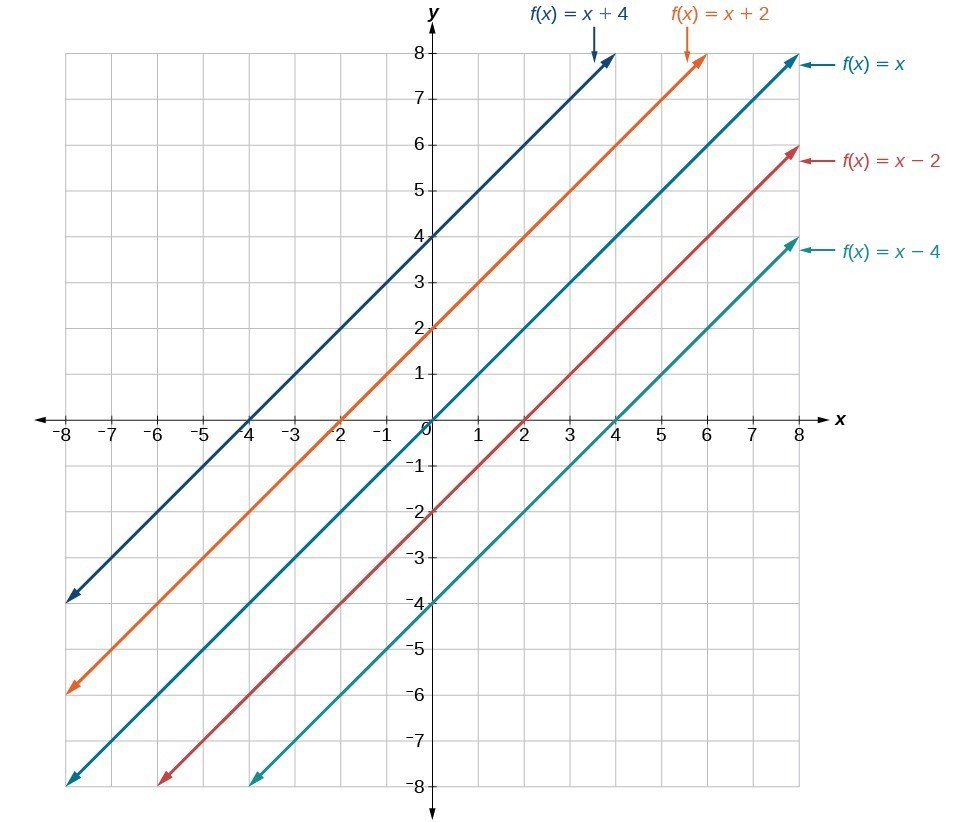
Transformations Left Or Right
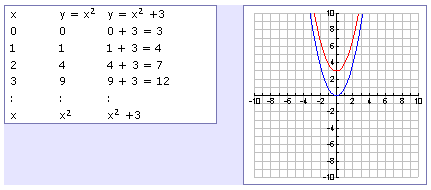
We have to graph the function using the rule for transformation Let us suppose the parent function is Below, is the graph of the parent function (fig 1) When we add some constant 'c' in the function then the graph of the parent function shifts upward by 'c' units Hence, when we add 2 then the parent function will get shifted upward by 2 unitsThis video explains how to determine the equation of an expoential function with a horizontal reflection and a vertical shifthttp//mathispower4ucomTransformations and Matrices A matrix can do geometric transformations!



How Do You Graph Y Sqrt X 1 And Compare It To The Parent Graph Socratic



1
Start studying Transformation Rules (x,y)> Learn vocabulary, terms, and more with flashcards, games, and other study toolsLinear Transformation Exercises Olena Bormashenko 1 Determine whether the following functions are linear transformations If they are, prove it; A simple transformation (confusion) from standard uniform distribution to Triangular distribution 2 What goes wrong in the product distribution of two iid



Graphing Quadratic Equations Using Transformations



Content Geometric Transformations Of Graphs Of Functions
43 Exploring Transformations of Quadratic Functions Parent Function of a quadratic function is f (x) = x 2 same as y = x 2 VERTEX FORM of a Quadratic Equation f (x) = ±a (x − h) 2 k The ± and ' a ' Value (Shape Factor) Function Value of a in f(x) = ax 2 Direction of Opening Vertex Axis of Symmetry Congruent to f(x) = x 2 f(x) = x 2



How Do You Identify Transformations In Parent Functions Given Y 2sqrtx 5 Socratic




Transformations Of Quadratic Functions College Algebra




Parent Function Worksheet 2




Transformations In Math Definition Graph Video Lesson Transcript Study Com




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
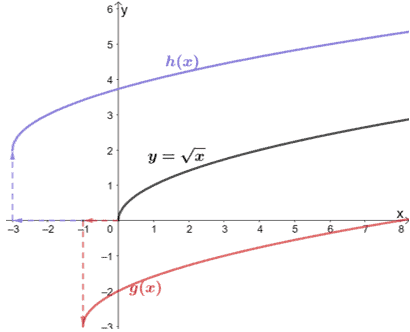



Transformations Of Functions Explanation Examples



Parabola Transformations Zona Land Education



Biomath Transformation Of Graphs
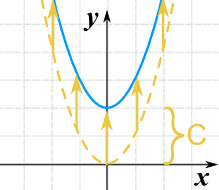



Function Transformations
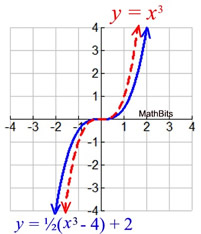



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math
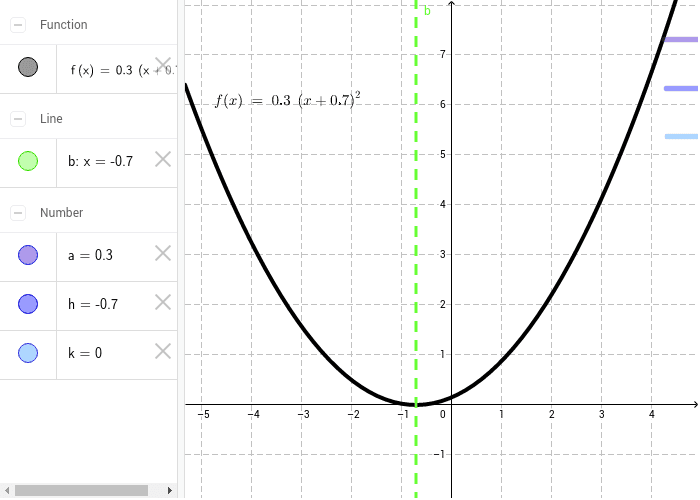



Transformations To The Graph Of Y X 2 Geogebra
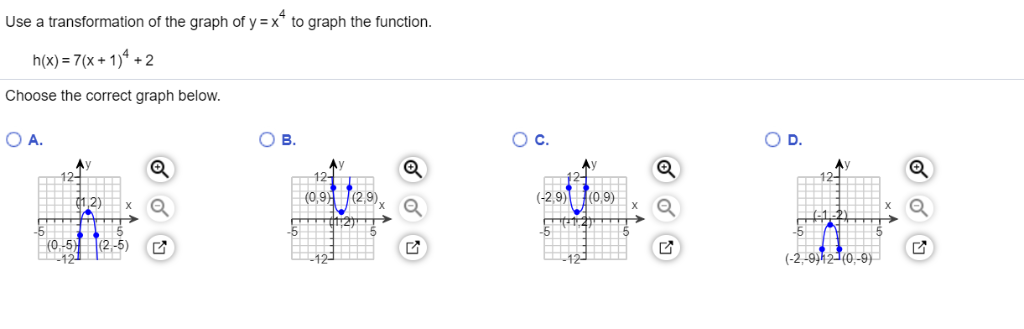



Solved Use A Transformation Of The Graph Of Y X 4 To Grap Chegg Com
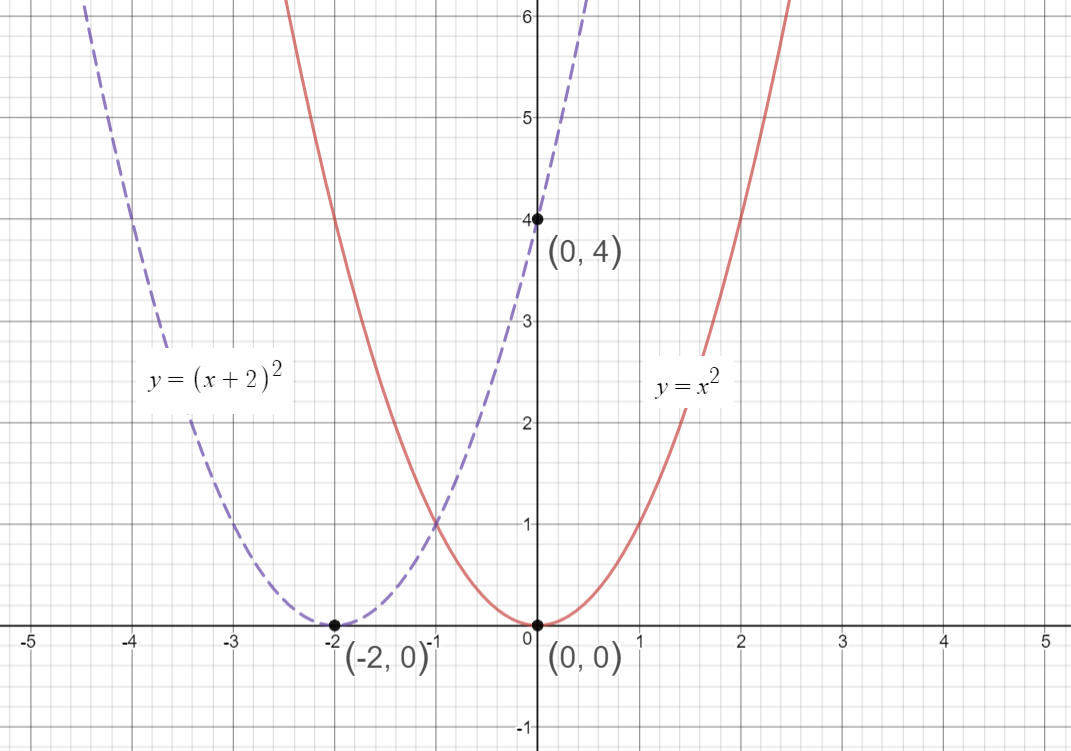



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic




Content Transformations Of The Parabola




Transformations Of Functions Ck 12 Foundation
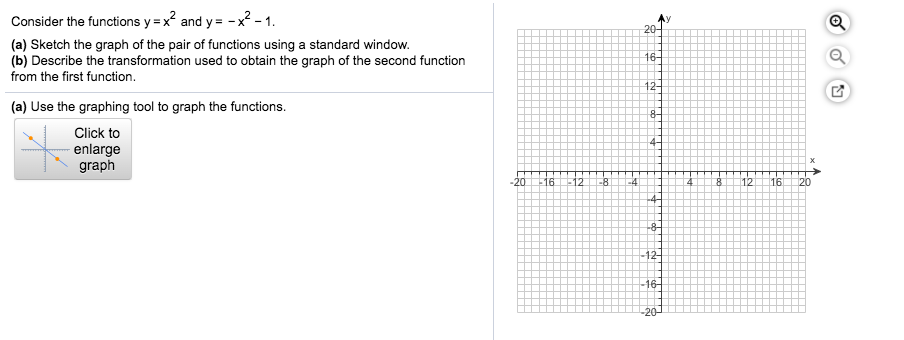



Solved 16 O Consider The Functions Y X And Y X2 Chegg Com
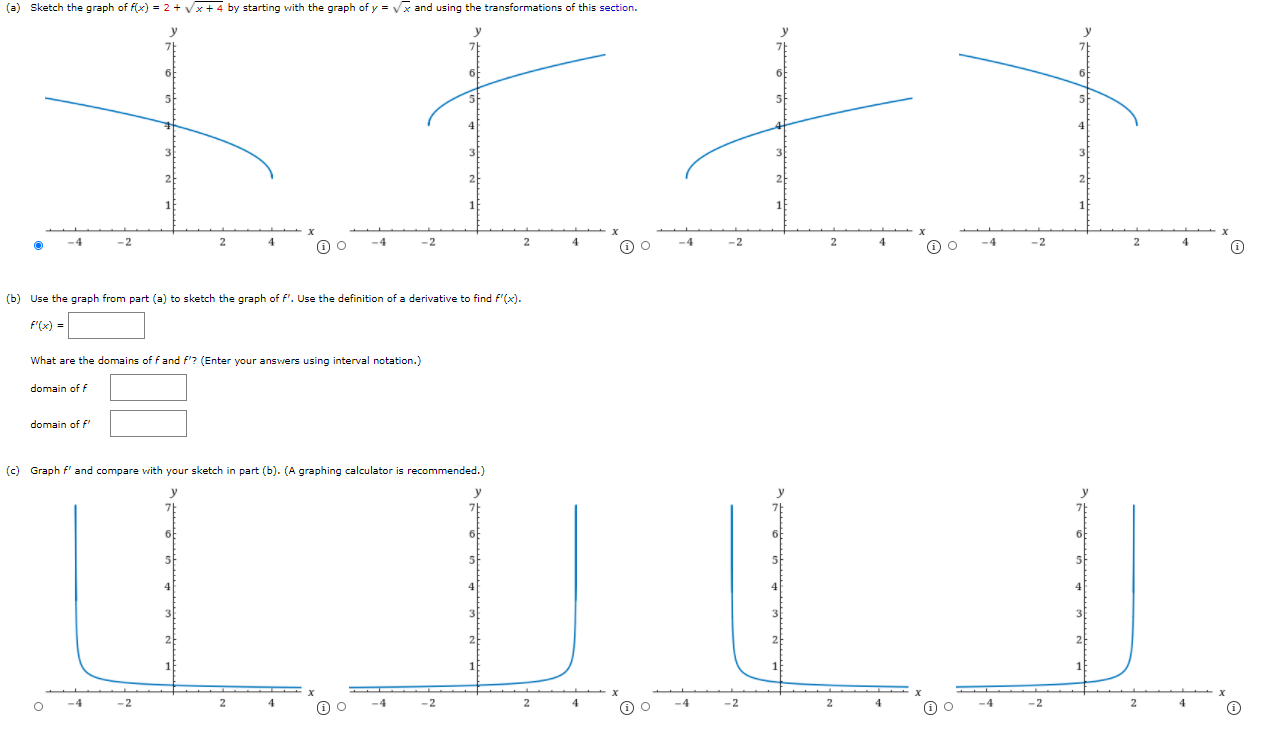



Solved A Sketch The Graph Of F X 2 X 4 By Starti Chegg Com



1



Transformations Of Functions Explanation Examples




Combining Transformations Ck 12 Foundation




Functions Transformations Isaac Physics



1 The Graphs Of Many Functions Are Transformations Of The Graphs Of Very Basic Functions The Graph Of Y X 2 Is The Reflection Of The Graph Of Y X Ppt Download



Transformations




Function Transformations Horizontal And Vertical Translations Youtube




Identifying Vertical Stretch Or Shrink



Search Q Vertical Compression Tbm Isch
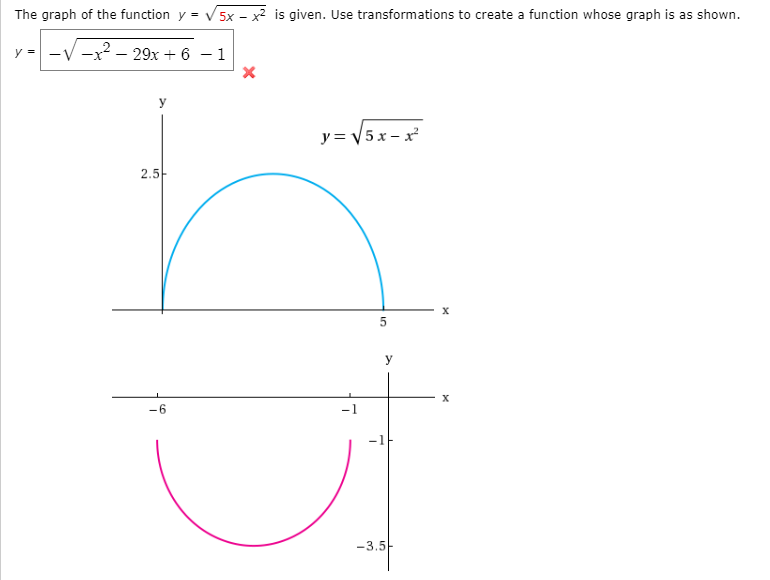



Answered The Graph Of The Function Y V 5x X Bartleby



Transformations Of Functions Explanation Examples



Search Q Parabola Equation Tbm Isch



Transformations Of Functions Explanation Examples




View Question 1 Describe The Transformation Done To The Parent Function Y 2x In Each Equation Below



Read Transform Linear Functions Intermediate Algebra




Content Transformations Of The Parabola



Algebra 2 Transformations Of Functions Pt 1 Youtube



Transformations Of Functions Refresher Mathbitsnotebook Ccss Math



How Do You Sketch The Graph Of Y X 2 2 2 And Describe The Transformation Socratic



Desmos 2 Transformations Of Graphs Cambridge Maths Hub




Transformations Of Y X Ck 12 Foundation



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math
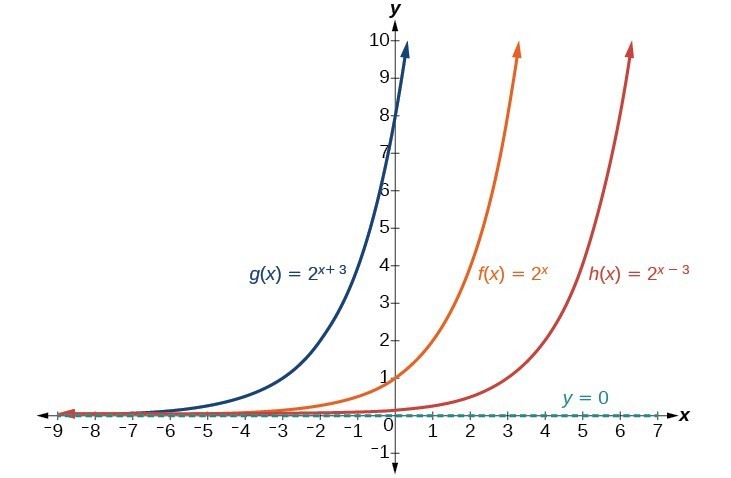



Graph Exponential Functions Using Transformations College Algebra




Symmetry Transformations And Compositions
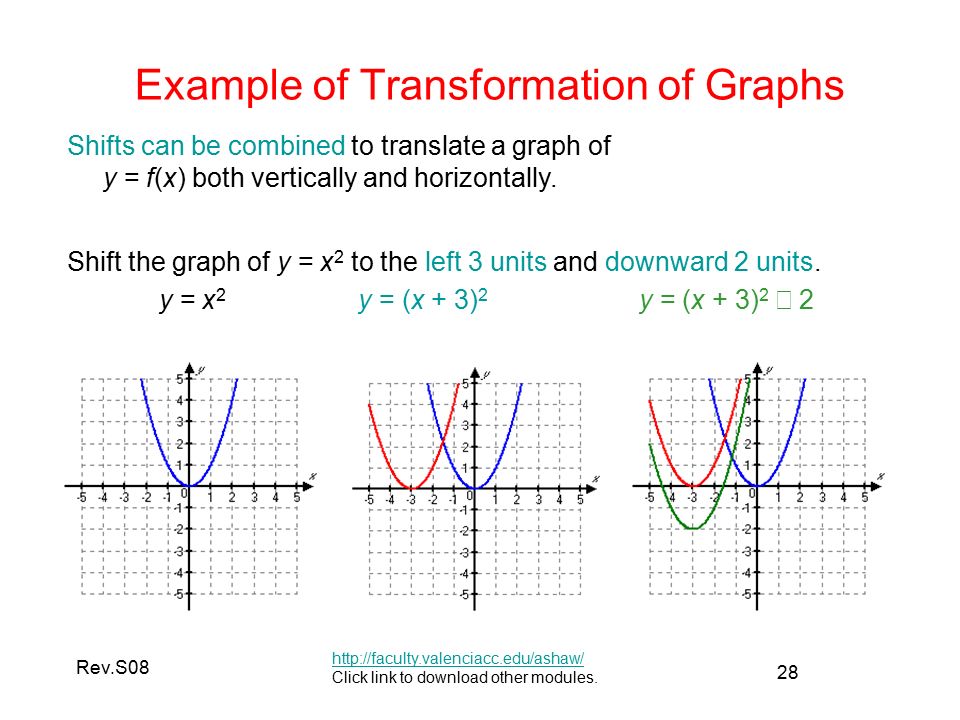



Transformation Of Graphs Ppt Video Online Download
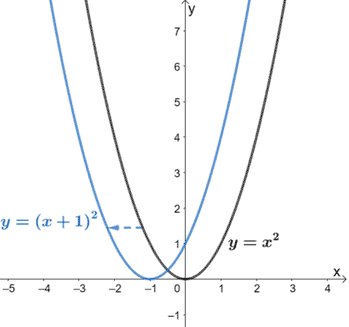



Transformations Of Functions Explanation Examples




Which Sequence Of Transformations Produces A Congruent Figure Note Each Answer Choice Represents A Brainly Com
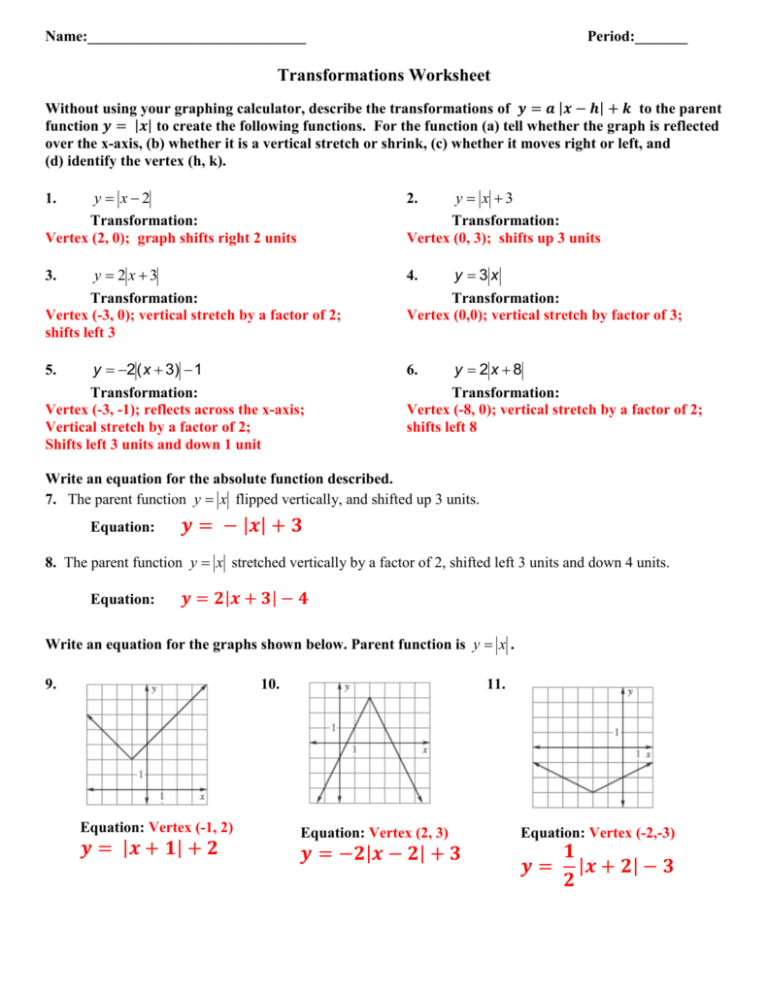



Absolute Value Transformations




Sketch The Graph Of The Equation Y X 2 2 3 Study Com
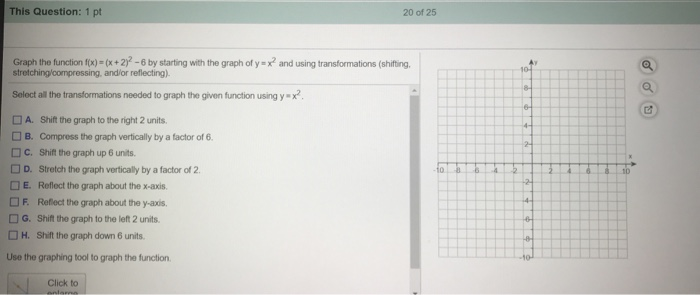



This Question 1 Pt Of 25 Graph The Function F X Chegg Com
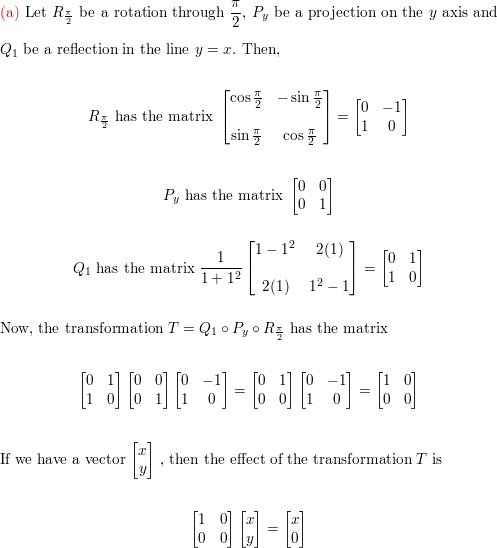



Determine The Effect Of The Following Transformations A Rotation Through Frac Pi 2 Followed By Projection On The Y Axis Followed By Reflection In The Line Y X B




Grade 10 Transformations Of Y X 2 Youtube




Transformations With Functions And Relations



Vce School Notes Graph Transformations
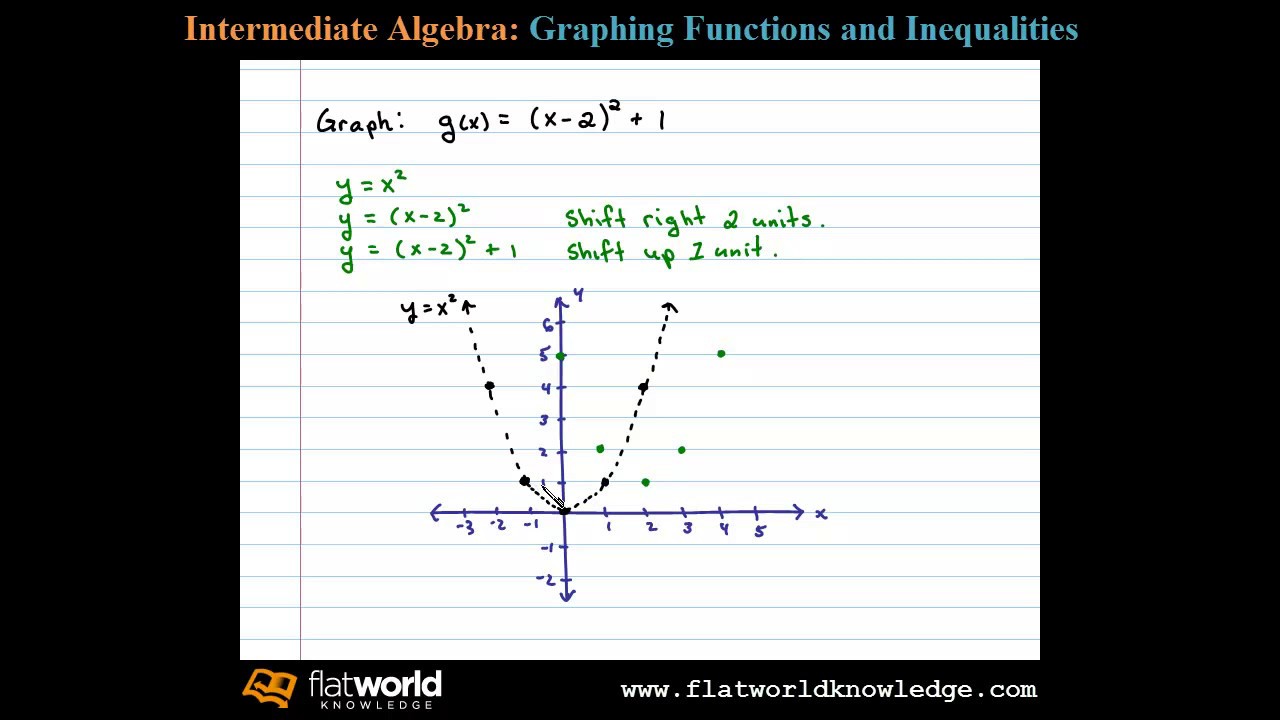



Graph Using Translations G X X 2 2 1 Transformations Algebra Fwk Ia 02 0501 Youtube



Graphs Of Quadratic Function Introducing The Concept Transformation Of The Graph Of Y X Ppt Download
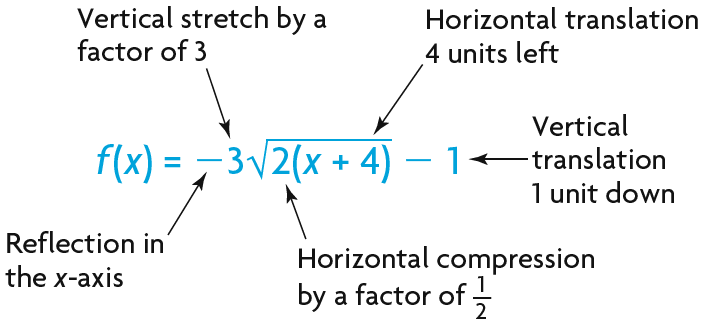



Using Transformations To Graph Functions Of The Form



Transformation Of Y X 2 And Y X 3 Geogebra



Transformations Of Y X 2 Using Desmos Teaching Resources
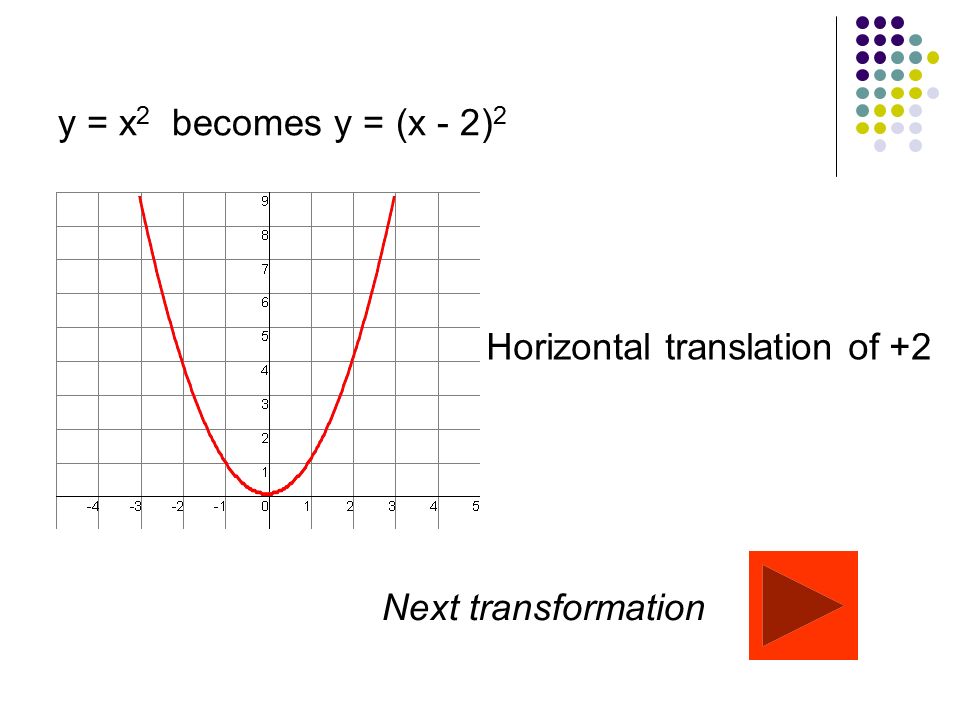



Transformations For Each Slide Choose The Correct Answer From The List Of Choices Using The Mouse Cursor All Slide Transitions And Animations Use A Left Ppt Download



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic



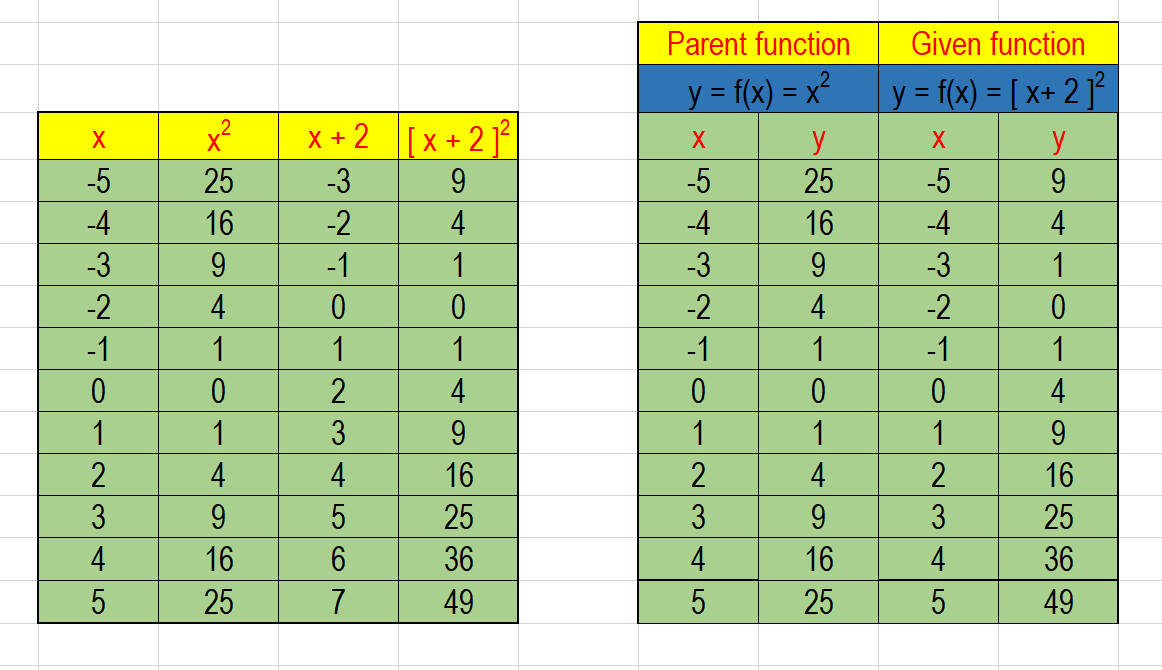
Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math




Algebra 2 Transformations Of Parent Functions Youtube
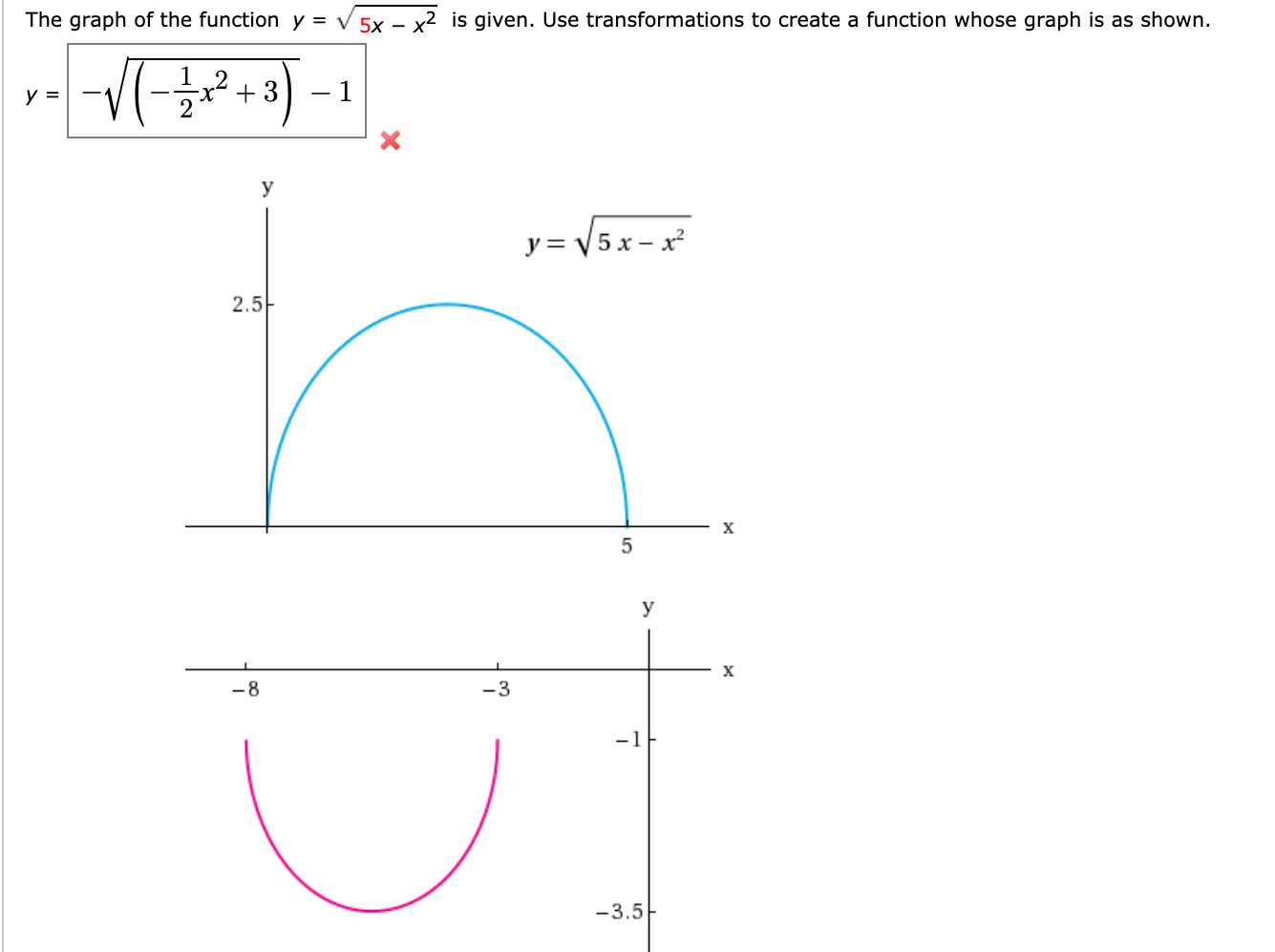



The Graph Of The Function Y V 5x X2 Is Given Use Chegg Com




1 07 Transformations Of Functions
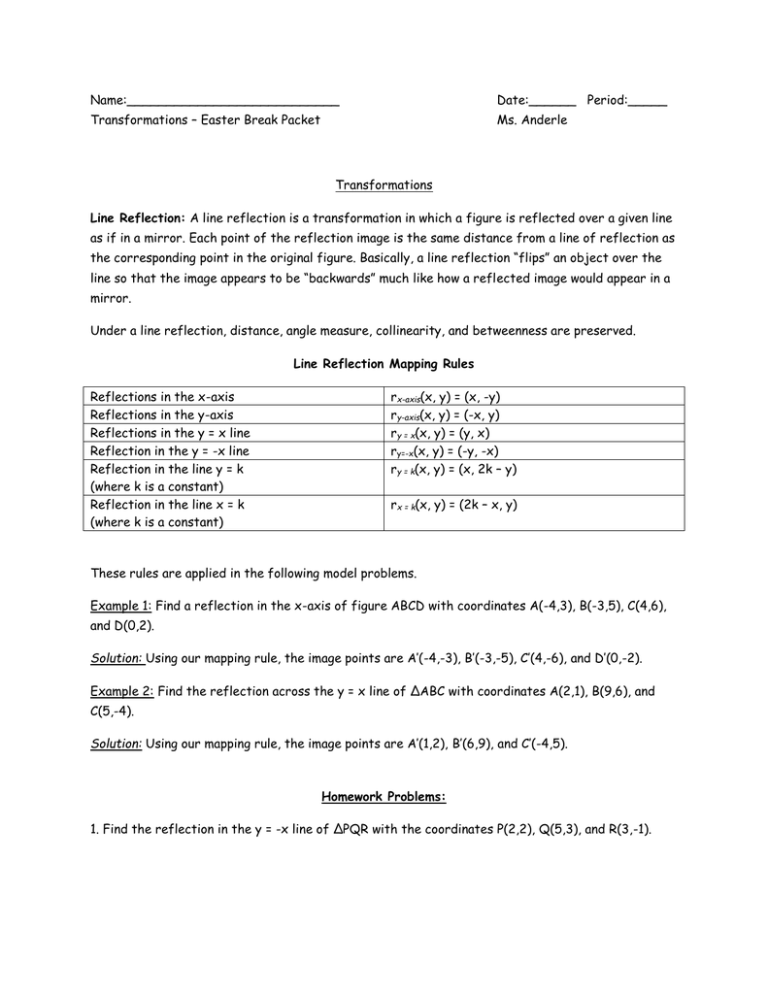



Name Date Period Transformations Easter Break Packet




Describe How The Graph Of Y X 2 Can Be Transformed Chegg Com
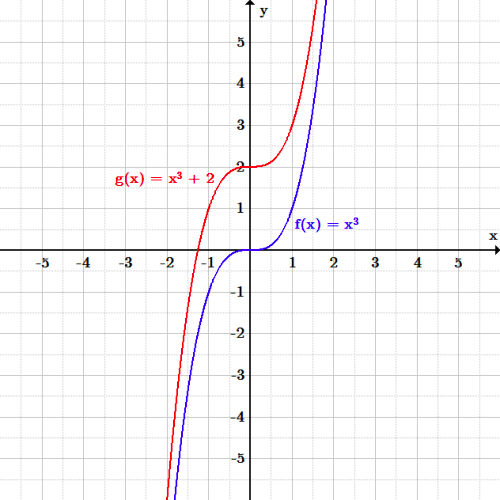



Transformations Boundless Algebra
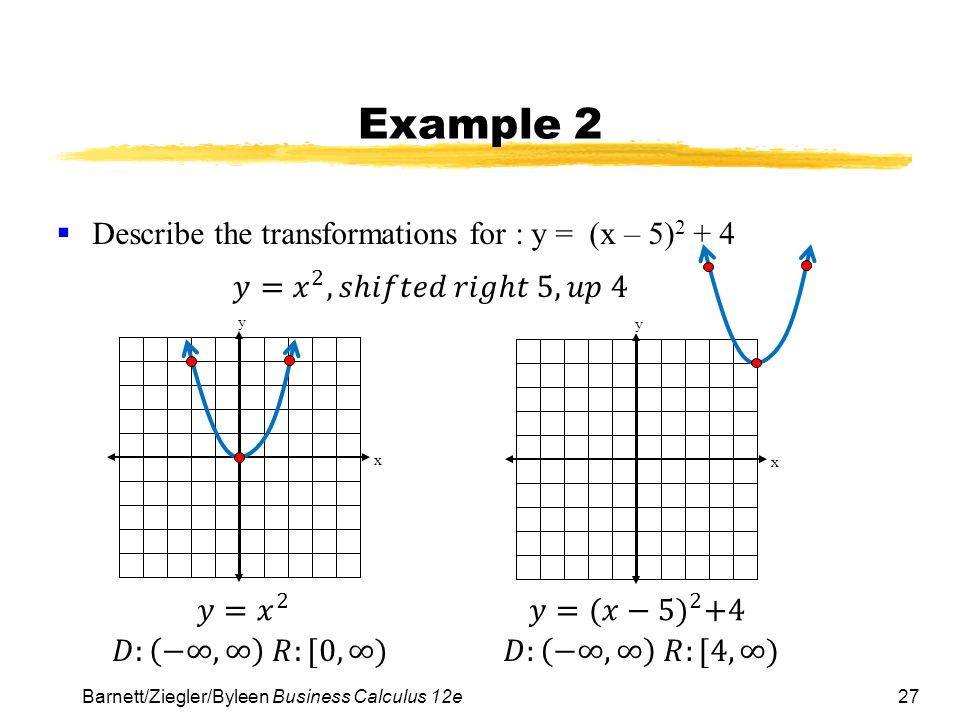



Chapter 2 Functions And Graphs Section 2 Elementary Functions Graphs And Transformations Ppt Download




Transformations Of Y X Ck 12 Foundation




How To Graph Transformations Of Functions 14 Steps
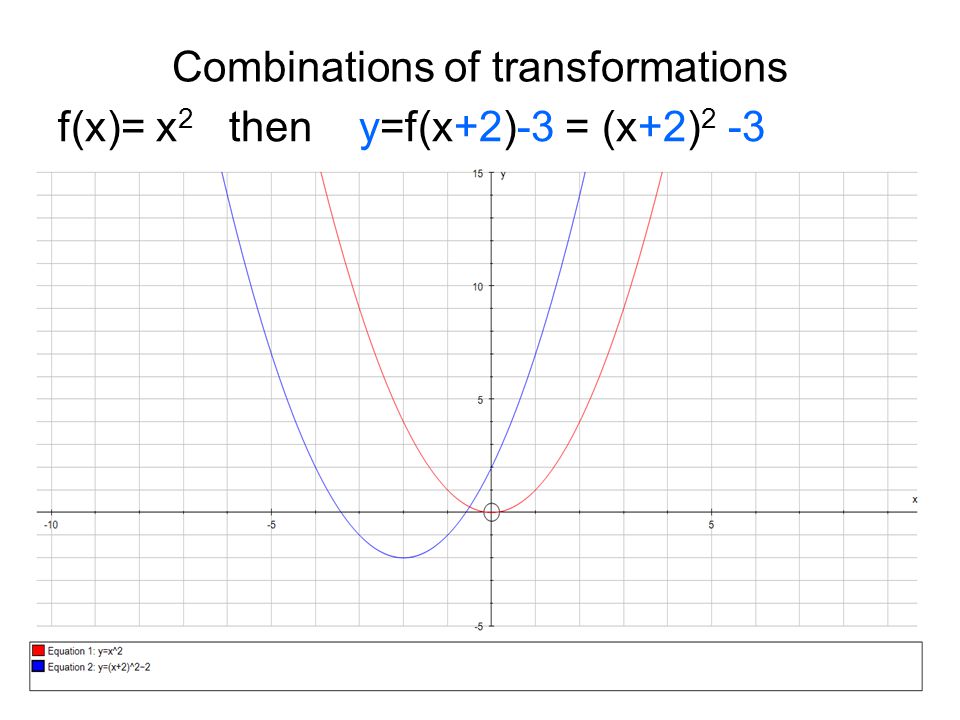



Transformation Of Graphs Andrew Robertson Transformation Of F X A F X X Ppt Download
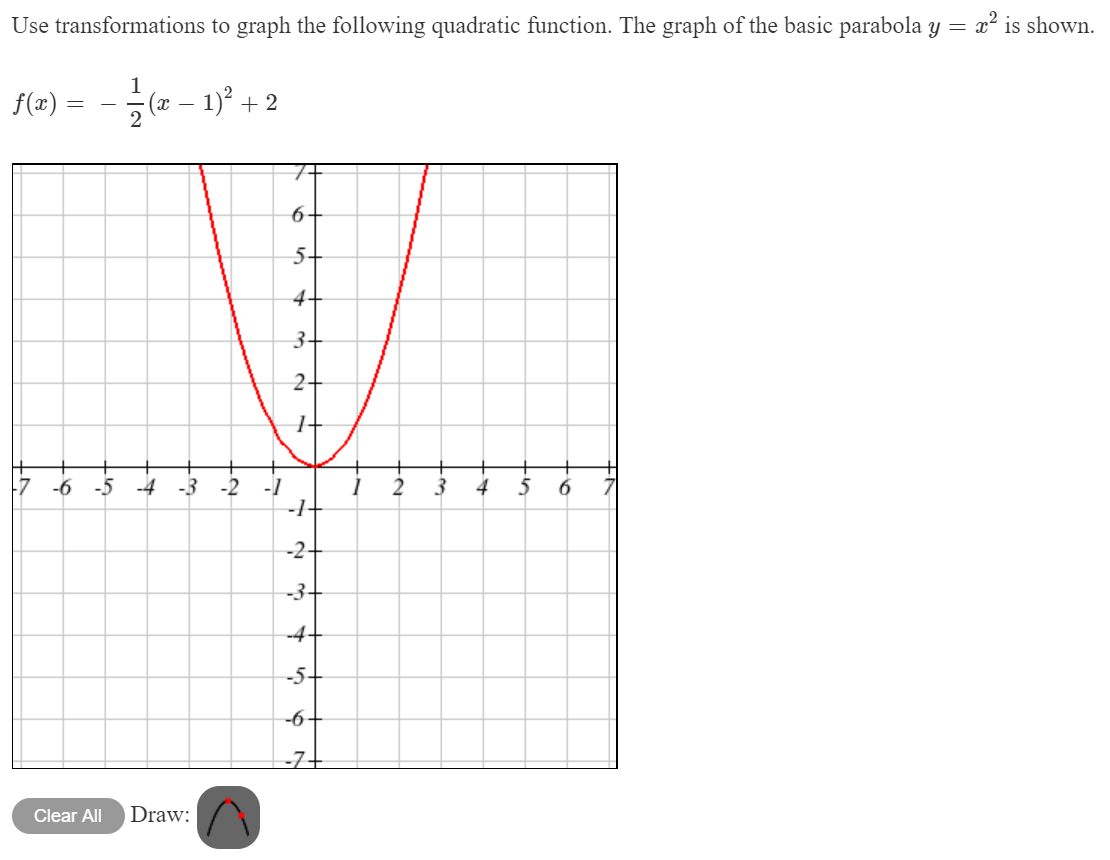



Use Transformations To Graph The Following Quadratic Chegg Com
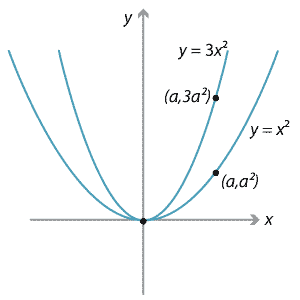



Content Transformations Of The Parabola
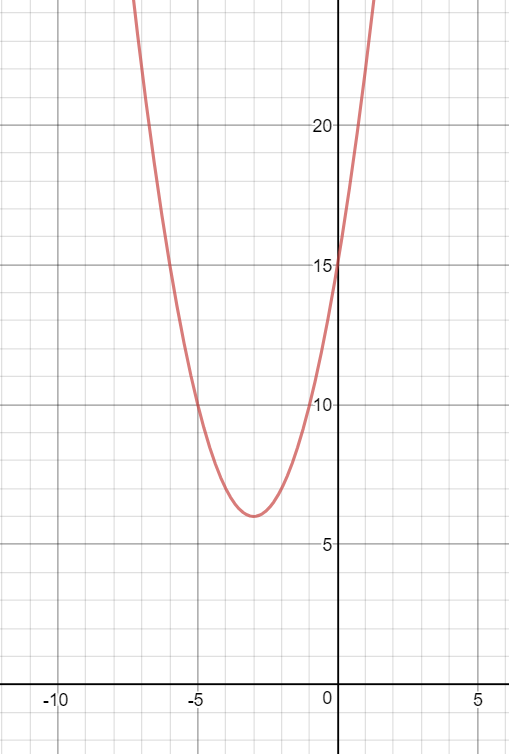



How Do You Sketch The Graph Of Y X 3 2 6 And Describe The Transformation Socratic




Content Transformations Of The Parabola
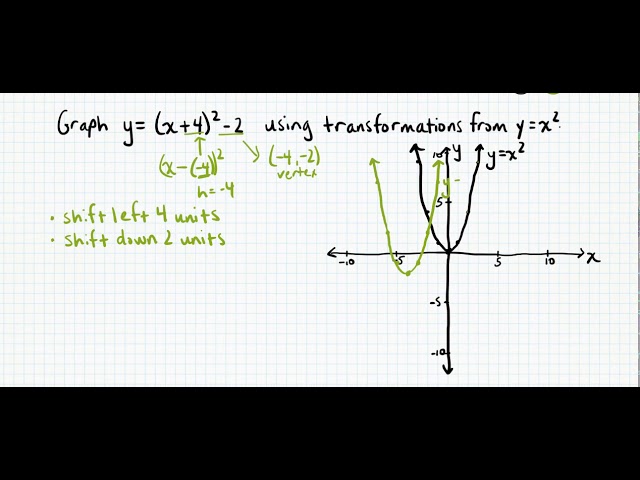



Graphing Transformations Of Y X 2 Youtube




Using Transformations To Graph Functions




The Graph Of Y Sqrt 4x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Below Study Com
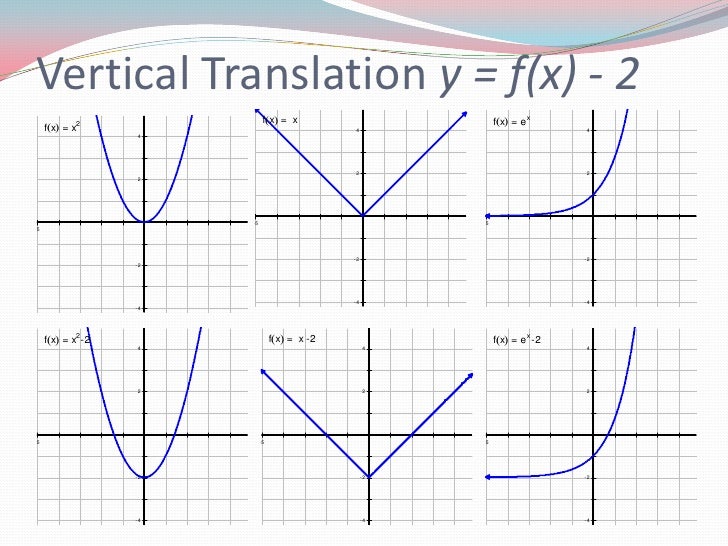



Transformations
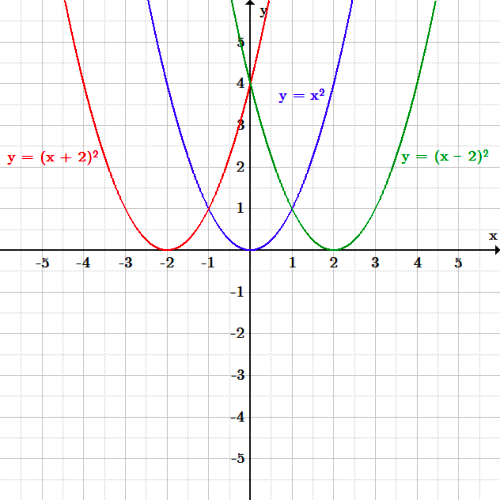



Transformations Boundless Algebra


