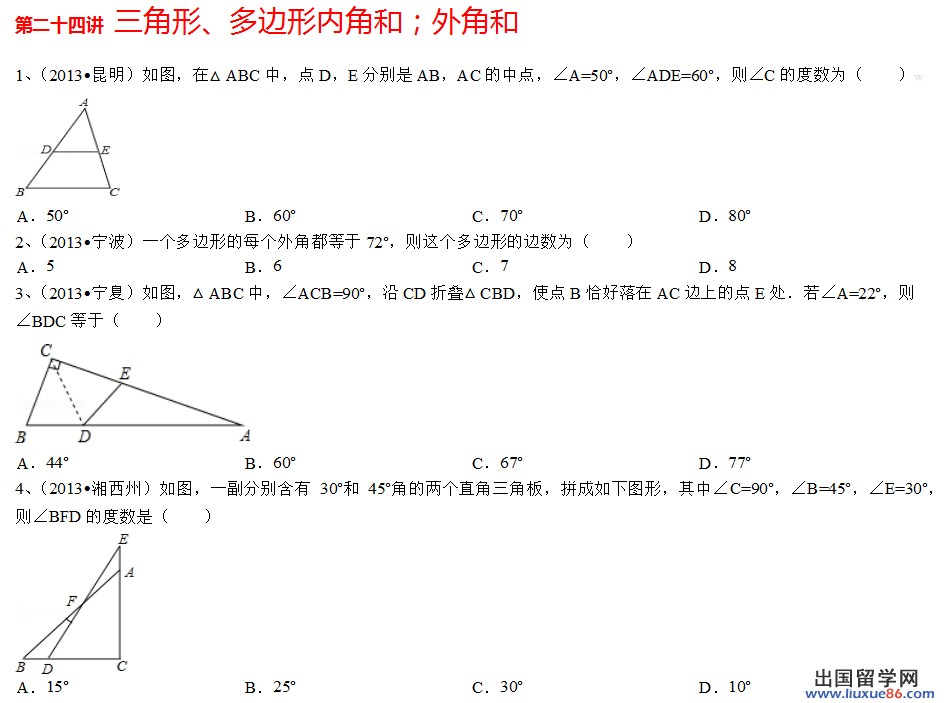
今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ=となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質 2在在ABC中,中, 1C90,A30 ,则,则B; 2A50 ,BC,则,则B 1三角形三个内角的和等于多少度三角形三个内角的和等于多少度 3在中,在中, :则:则, 40 60 80 65 60 三角形的内角和等于三角形的内角和等于,新文库网xinwenkucom内角の和の公式から 正十五角形だと分かるので1つの外角は 図の の大きさを求めなさい。 補助(延長)線を引いて内角の和などを利用して求まります。 こういう形をした多角形を凹多角形といいますが、気にしなくて良いです。 笑 四角形や三角形に

三角形内角和定理 平行线的证明ppt课件4下载 牛二ppt
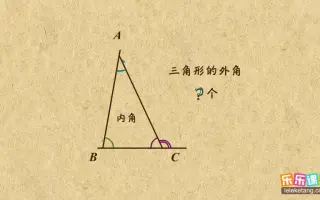
三角形内角外角
三角形内角外角-重点:三角形的外角及其性质 难点:运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法。 三、教材分析: 教材由学生已经熟悉的三角形的内角和定理引入,然后探索三角形外角的性质。 三角形内角和与外角和定理 2141 0 7 0 详细信息 id 分类: 试题试卷 , 同步练习 , 全国 , 21 资源大小:475kb 资料长标题:三角形内角和与外角和定理 2122学年人教版八年级上册数学



数学老师手抄版 初二数学 三角形内角与外角 经典题
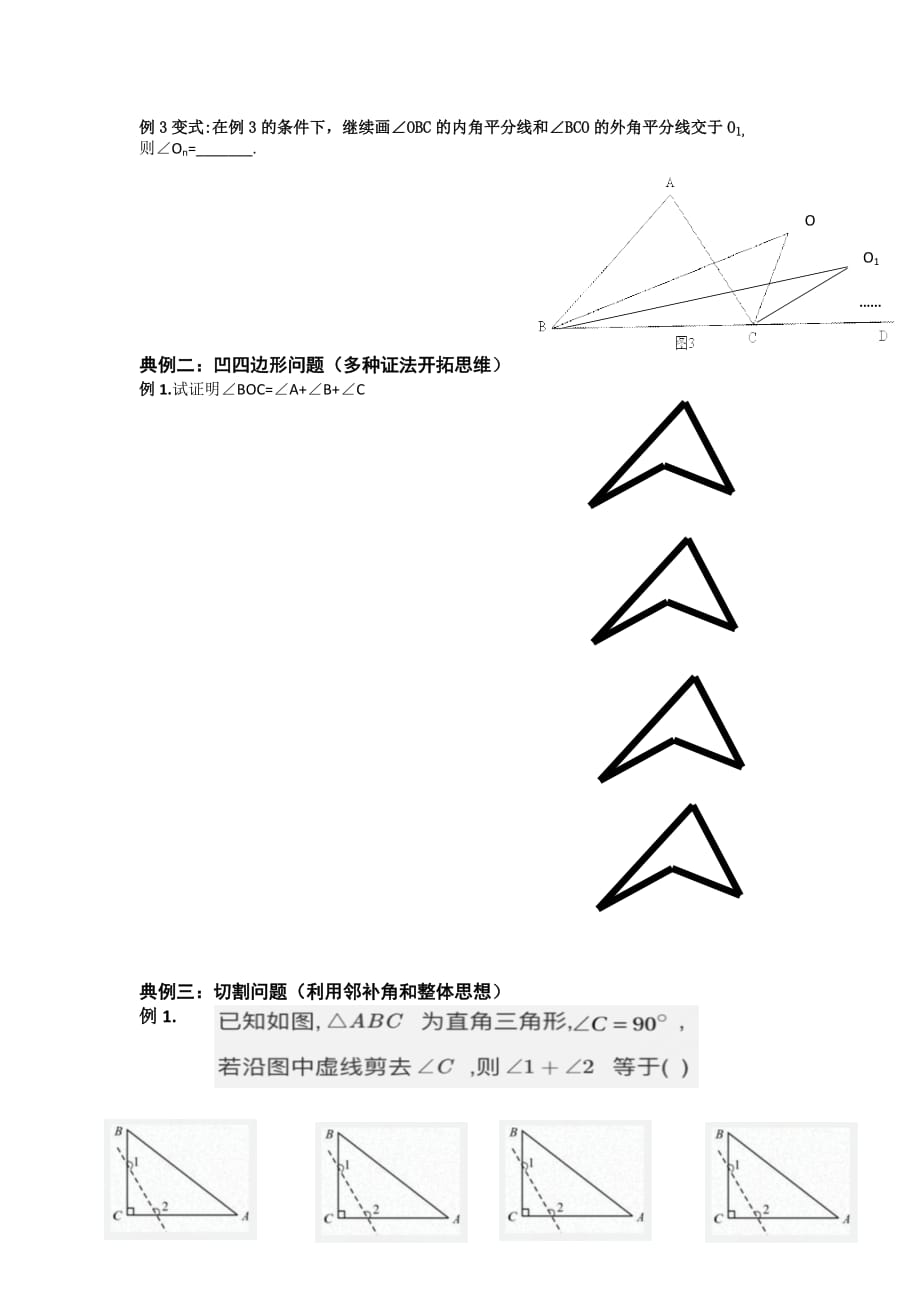
多学多练,熟能生巧!我们今天解析两道三角形内外角平分线综合题,准备知识如下: 1) 三角形内角和180° 2) 三角形外角的度数等于不相邻的两内角度数之和 3) 角平分线上的点到角两边的距离相等,反之亦 内角と外角の関係を使った解答 まずは、内角と外角の関係を使って 赤文字 部分を出します 補助線を引いてできた右下の小さい にも 内角と外角の関係を使って x 35 = 155 x 35 = 155 ∴ x = 100 x = 100AYX爱游戏app体育官方下载 为你整理了多篇七年级下册《912 三角形的内角和与外角和》教学设计,但愿对你工作学习有帮助,当然你还可以在AYX爱游戏app体育官方下载 找到更多七年级下册《912 三角形的内角和与外角和》教学设计。
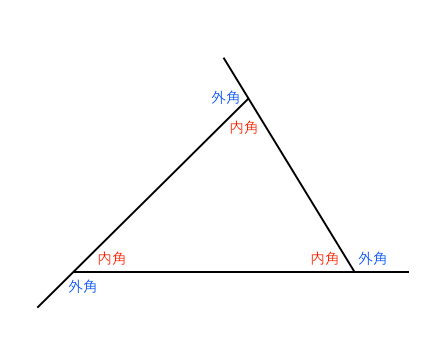
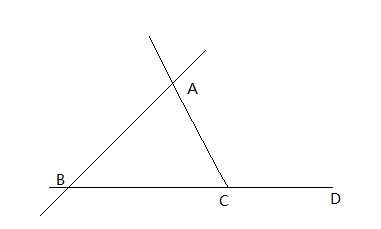
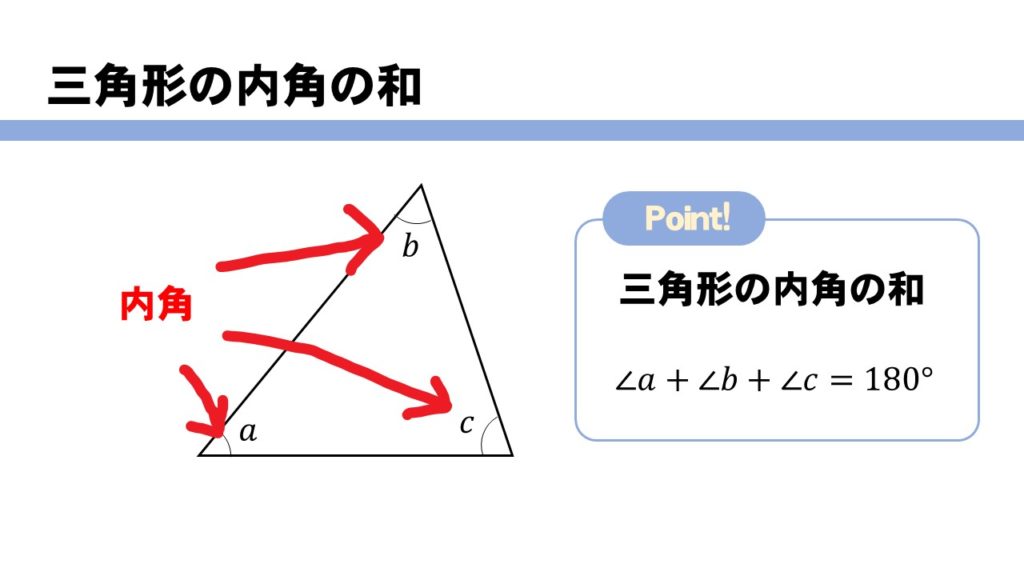
三角形の内角と外角 $ ABC$ において,$\angle A,\angle B,\angle C$ を,$ ABC$ の内角といいます. また,下図の $\angle ACD$ や $\angle BCE$ のように,一つの辺とその隣の辺の延長がつくる角を,外角といいます. さて,三角形の内角と外角について,次の重要な事実が成り立ちます.三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。 多角形の内角の和と外角の和の公式 n角形の内角の和:180°×(n−2)180°×(n−2) 多角形の外角の和:360°360° 難しく感じるかもしれませんが、内角の和は三角形が180°。 そこから角が増えるごとに内角の和も180°ずつ増えていきますよーということです。
三角形の内角・外角 中2数学 三角形の外角の定理については、意外と忘れられやすいのですが、とてもよく使いますし、便利なものなのでぜひ覚えておき、いつでも使えるようにしましょう。 また、今回のプリントは今後いろいろ応用を利かせる 三角形の外角 赤色の角度のことを、ぜんぶ 「外角」 と呼ぶよ! 三角形の1辺を延長して外角を理解しよう! 三角形の1つの外角は、その隣にない2つの内角の和と等しい はい。これ意味わかる・・・?クソわかりづらいよね?ウンウン。。 下の図で解説三角形・四角形の内角と外角 三角形、四角形の外角を知り、外角の和が360°を確認する ABCの外側にあるので ∠Cの外角 といいます。



三角形外角等于内对角之和



Word版 巧用三角形的外角以及三角形内角和公式的变形来解决三角形中角的有关求解与证明 7 2与三角形有关的角 初中人教版 数学中国网
多角形の内角の和と外角の和の公式をまとめると以下の通り。 N角形の内角の和:180°× (N −2) 180 ° × ( N − 2 ) 多角形の外角の和:360° 360 ° 内角の和は三角形の180°から、角が増えるごとに180°ずつ増えていきます。 それに対し、外角の和は角が 三角形内角和、外角练习题_优选pdf,word 类型一:三角形内角和定理的应用 1.已知一个三角形三个内角度数的比是 1:5:6,则其最大内角的度 数为( ) A.60° B .75° C .90° D .1° 举一反三: 变式 1在 ABC中,∠A=55°,∠B 比∠C 大 25 °,则∠ B 的度数为( ) A.50° B .75° C.100° D .125多角形はどのように区別がされているかというと、この角の数によってされています。 左から「三角形」「四角形」「五角形」です。 また、図形の内側の角を 内角 といい、それから延長した辺と1辺がつくる角を 外角 といいます。 この2つの角度を足す



三角形内角和定理 Ppt教学课件 第1课时 第一ppt
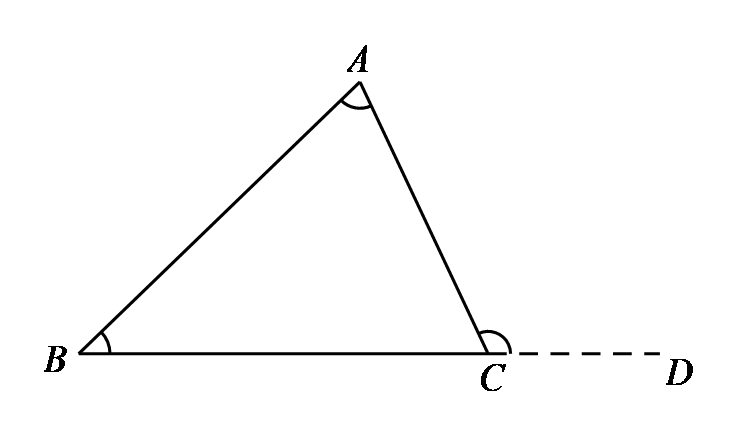



三角形内角和图片 搜狗图片搜索
三角形内角和八年级数学学科备课年级 八 班级 160 时间 1013 课题 三角形的内角和与外角性质 备课人 石宇霞 第1课时 教学目标 知识与技能掌握三角形内角和定理及其推论;了解三角形的分类,会按角的大小对三角形进行分类;了解直角三角形的分类;掌握三角形外角性质;初步学会使用辅助线三角形の外角の定理 『外角は、その外角のとなり以外の2つの内角の和に等しい』 つまり、下の図の通り。 外角の定理のひみつ外角= + ①三角形の内角の和は180度でした。 だから、三角形按角分类2三角形内角、外角的关系,会进行角度的计算和大小的比较 学习难点 外角性质的语言论述过程。 学习过程 b a c d 一、 知识回顾: 1、请在右图标出的四个角中,指出三角形的内角、外角.简诉三角形外角的定义。




三角形的内角和外角 Ppt课件下载 牛二ppt
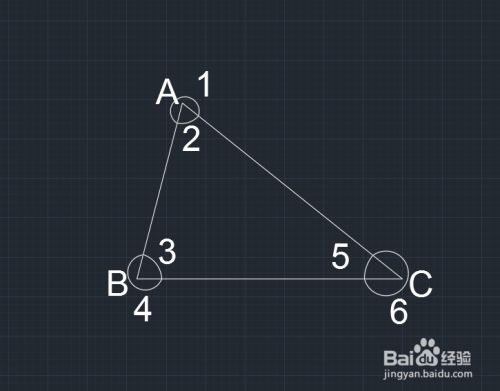



三角形外角和证明方法 百度经验
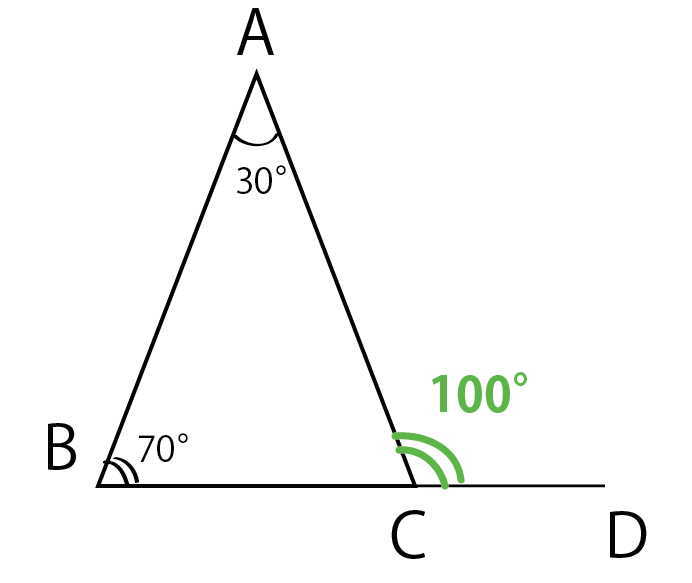
三角形の外角はそれととなり合わない2つの内角の和に等しいので ∠ABE = 50°23°=73° B 41° 17° A D x 50° 23° C E 58° ABDにおいて 三角形の外角はそれととなり合わない2つの内角の和に等しいので ∠CBD = 41°17° = 58° x 41° 17° A D 50° 23° B C E 73° 58° x = 180° 58°73如图,在 abc中,cd与cf分别是 abc的内角、外角平分线,df∥bc交ac于点e.试说明:(1) dcf为直角三角形;(2)de=ef. 正三角形の1つの内角は60°、外角は1°なので、 外角の和は1°×3=360° 「あっ、そうそうそうそう、外角の和は360°だったね~」 と思い出そう!! 多角形の外角の和を忘れたら、正三角形で検証せよ!! 問題 図に示された角度は、全て三角形の外角だね?




五边形内角和 五边形的内角和是多少度 52fmz购物网



三角形的内角和定理 外角的性质 07年中考题集锦 7 2与三角形有关的角 初中人教版 数学中国网
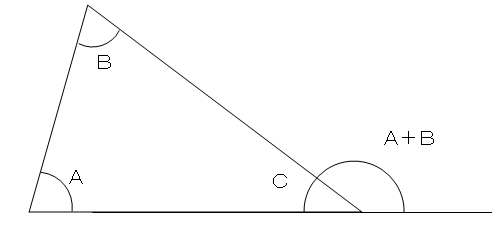
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru外角定理(がいかくていり)とは、三角形の外角はそれと隣り合わない2つの内角の和に等しいということを示す、ユークリッド幾何学における定理。 その形状から、「スリッパの法則」と呼ばれることもある 要出典 。 証明そして、「三角形の内角の合計は180度」です。 (角a)+(角b)+(角c)=180度 そして 以上のことを利用し、外角にとなり合わない2つの内角を下の図のようにあてはめてみます。 このようにすると一目で分かります。



内角总和
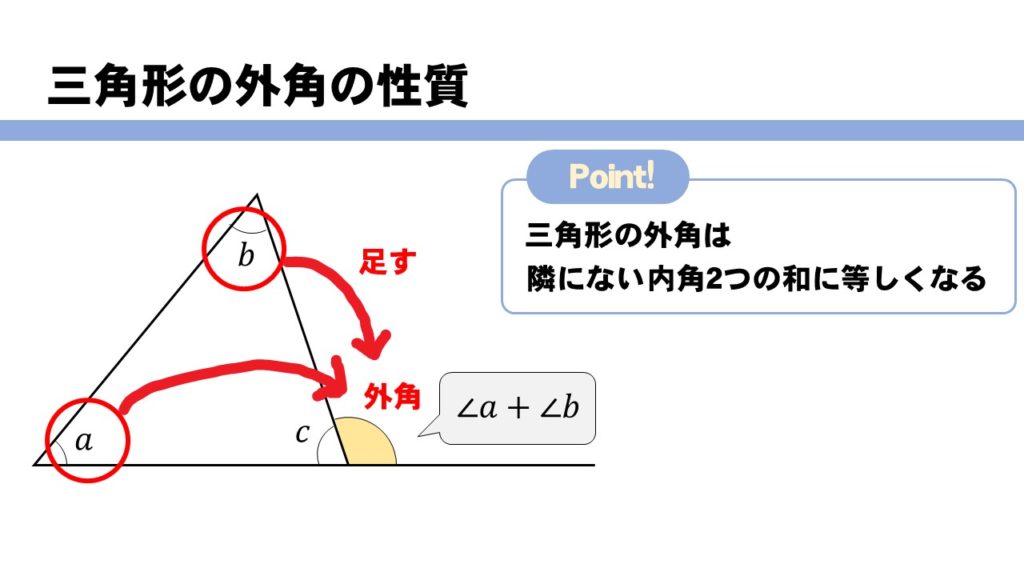



3分なるほど 三角形の内角 外角の性質について解説 数スタ
已知三角形的一个外角等于与它相邻的内角的2倍,且等于与它不相邻的一个内角的4倍,这是什么三角形 把命题"三角形的一个外角大于与它不相邻的任何一个内角"改写成"如果···那么···"的形式是( 用反证法证明 同位角相等 两直线平行能用三角形外角三角形の内角と外角 17M views Discover short videos related to 三角形の内角と外角 on TikTok Watch popular content from the following creators 楽しく勉強あきとんとん(@akitonton), ふたっちょ(@futacho), カリスマ講師の数学クラス(@charismateacher), 学習塾We'lll(@jukuwelll), 楽しく勉強あきとんとん(@akitonton)内角と外角を足すと180°になる という特徴があります。 これを使って考えると 正多角形の内角1つ分の大きさは $$\large{180(外角)}$$ このように求めてやることができます。 正三角形の場合




初一奥数第18讲三角形内角和经典例题 2 每日头条



1
こんにちは、ウチダです。 今日は、中学2年生で詳しく学ぶ 「三角形の内角の和」 について、それが180度である証明や、三角形の外角に関する公式・問題を解説していきます。 また、記事の後半では「内角の和が270度である三角形」についても考察し三角形 外角和为360°作为公认的劳模,平日里,超模君不但要码字,工作之余还要监督表妹做作业,也难怪表妹成绩总是能名列前茅。 今天表妹做作业时,遇到一道判断题: "三角形的内角和等于180°",她多角形の外角の和は、$\textcolor{blue}{360°}$ となります。 何角形であっても同じ $\textcolor{blue}{360°}$ です。 正三角形の場合を考えてみると、正三角形の $1$ つの内角は $60°$ なので、$1$ つの外角は、$180°60°=\textcolor{blue}{1°}$ となります。




3 三角形外角定理 简书



三角形一个内角与一个外角的角平分线夹角的度数初中数学八年级上册 哔哩哔哩 つロ干杯 Bilibili
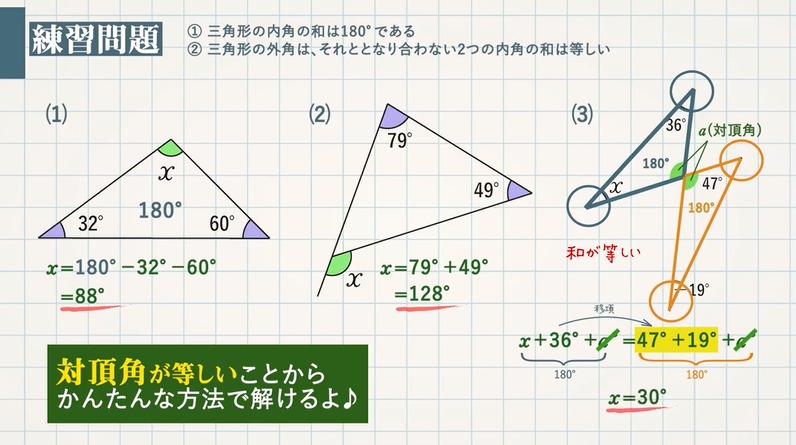
(1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。



数学老师手抄版 初二数学 三角形内角与外角 经典题



三角形的内角和外角 Ppt 第一ppt




七年级数学多边形内角和与外角和 三角形 基础练习 文库吧



八上数学证明 三角形的一个外角等于和它不相邻的两个内角的和 哔哩哔哩 つロ干杯 Bilibili



数学老师手抄版 初二数学 三角形内角与外角 经典题
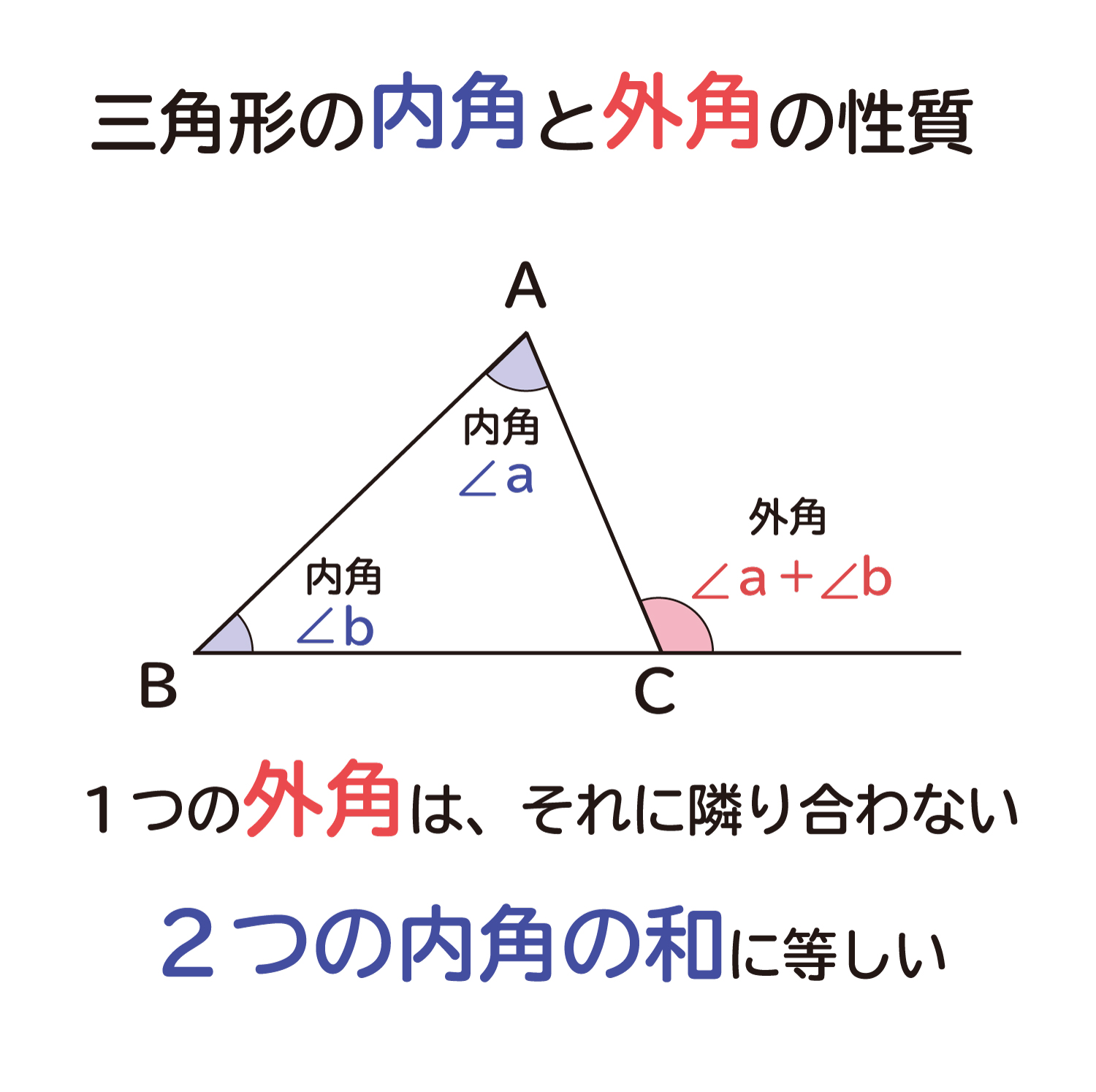



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル



数学老师手抄版 初二数学 三角形内角与外角 经典题



怎样证明三角形的外角大于任何一个不对应的内角 百度经验




七年级 三角形 内角和 外角 外角和定理



三角形内角与外角视频 西瓜视频搜索




三角形内角和定理 平行线的证明ppt课件4下载 牛二ppt



三角形内角与外角和典型例题 金锄头文库



三角形内角和是多少度 外角和度数是多少 初三网




3 三角形外角定理 简书



三角形内角和是多少度 初三网



70以上三角形内角外角 シモネタ




三角形的内角和与外角和 A 41 下载 Word模板 爱问共享资料



三角形的内角和外角 图片搜索



11 2 2 三角形的外角 人教版八年级上册数学电子课本 数九网




多边形的内角和与外角和 简书



怎样证明三角形的外角大于任何一个不对应的内角 百度经验



三角形的外角讲解 北京爱智康



三角形的内角和外角 图片搜索




七年级数学多边形内角和与外角和 三角形 基础练习 文库吧




三角形两角和等于外角 搜狗搜索
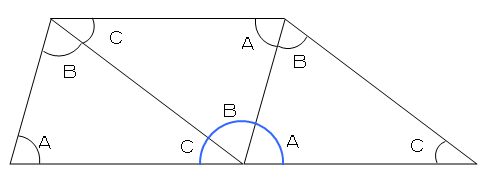



70以上三角形内角外角 シモネタ



三角形内角与外角视频 西瓜视频搜索
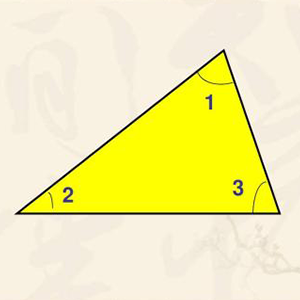



三角形内角和是多少度 搜狗指南




外角和与内角和 哔哩哔哩



数学老师手抄版 初二数学 三角形内角与外角 经典题
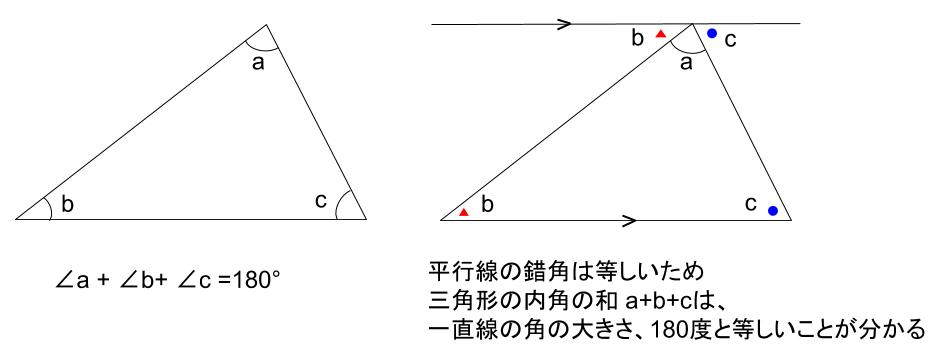



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




三角形内角和定理 平行线的证明ppt课件3 Ppt课件下载 人人ppt




多边形的内角



腾讯视频
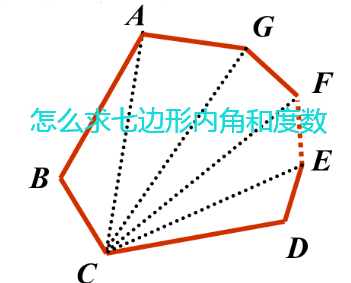



怎么求多边形内角和与外角和的度数怎么求七边形的内角和度数



内角和外角的图解 万图壁纸网



七下数学 三角形 内角和 外角 外角和定理 平行线



初一奥数第18讲三角形内角和经典例题 3 雪花新闻




多边形的内角
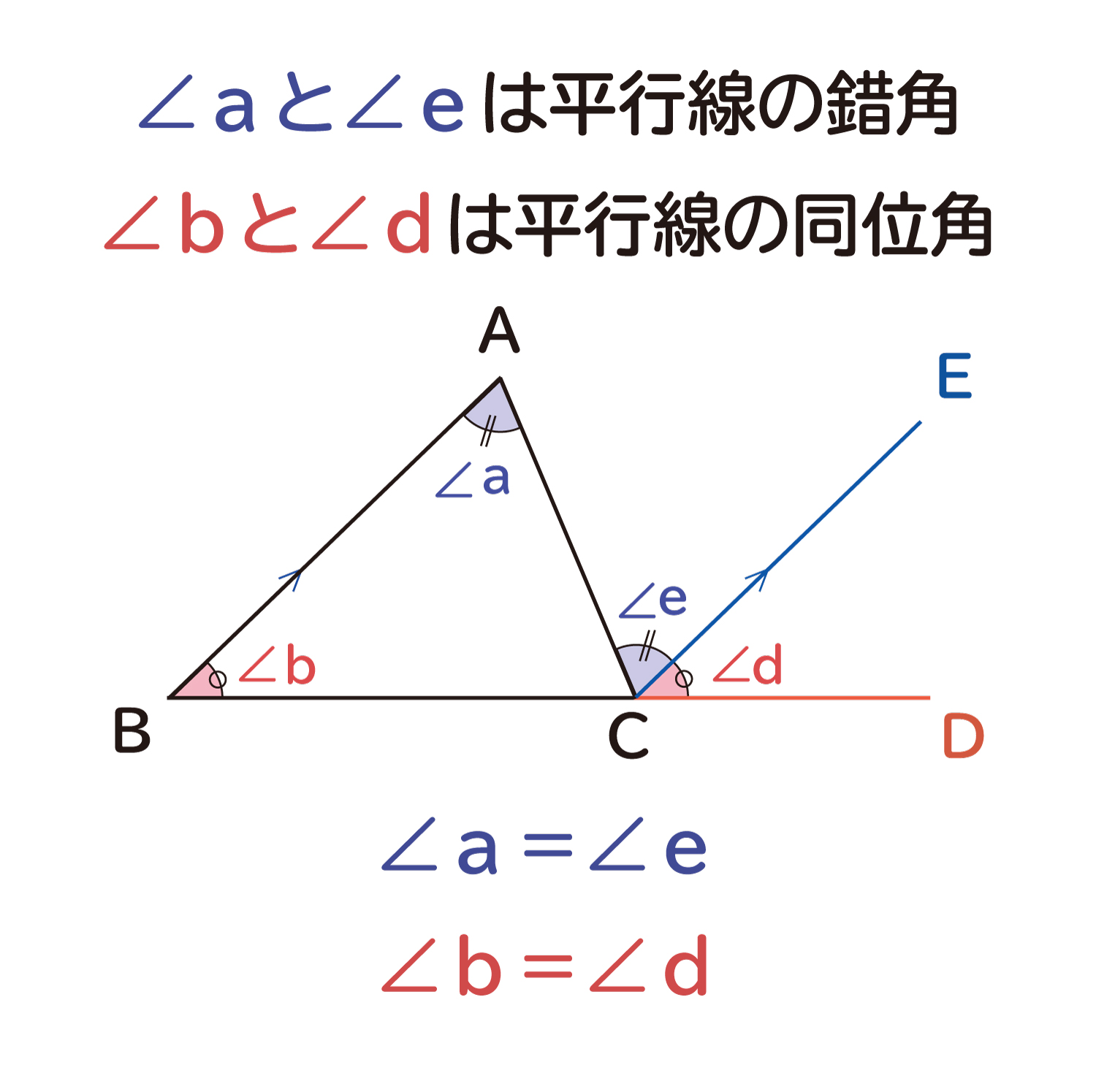



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル



从三角形的外角入手求角 9 2多边形的内角和与外角和 初中华师大版13版 数学中国网 Mathschina Com
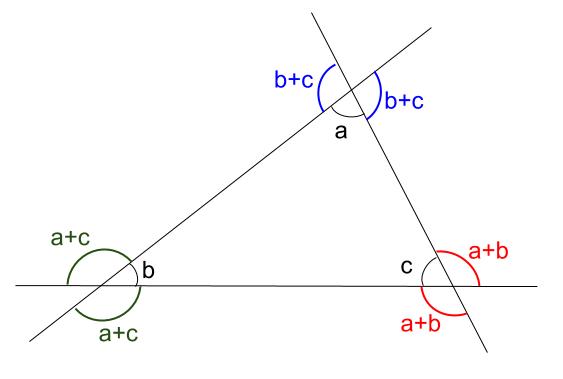



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




初中统考几何相似三角形 内角平分线与外角平分线的性质 老雷数学 Youtube




三角形的内角和外角和分别是多少 三角形的内角和和外角和是多少 三人行教育网 Www 3rxing Org




多边形的内角和与外角和 简书




多边形的内角和与外角和 简书



数学老师手抄版 初二数学 三角形内角与外角 经典题



三角形的内角和外角 Ppt课件 第一ppt




教师资格证面试 小学数学真题教案设计 知乎




通俗数学 三角形外角和等于360 优胜于 内角和等于180




多边形的内角和与外角和 简书
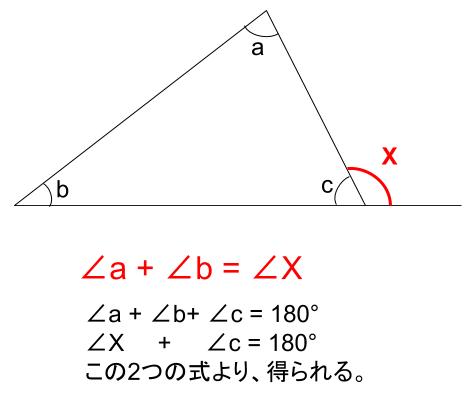



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



数学老师手抄版 初二数学 三角形内角与外角 经典题




06三角形内角和定理的证明平行线的证明初中数学初二 Youtube



利用三角形内角外角性质解决角度问题 哔哩哔哩 つロ干杯 Bilibili



三角形有几个夹角 西瓜视频搜索



70以上三角形内角外角 シモネタ



3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく




三角形外角和内角关系 1 三角形内角和外角有什么关系2 三角形内角和为什么等于180 三人行教育网 Www 3rxing Org




三角形内角和定理 平行线的证明ppt课件4 Ppt课件下载 人人ppt



三角形内角外角题目 三角形内角外角题目 Josspixskul



三角形内角与外角视频 西瓜视频搜索



七下数学 三角形 内角和 外角 外角和定理 平行线



70以上三角形内角外角 シモネタ



70以上三角形内角外角 シモネタ




数学 中2 48 三角形の内角と外角 基本編 Youtube




三角形の内角と外角の性質 教遊者




通俗数学 三角形外角和等于360 优胜于 内角和等于180




外角 搜狗百科



三角形の内角と外角の性質 教遊者




File 三角形の内角と外角 Png 维基百科 自由的百科全书



初中数学与三角形有关的角 掌握考点 明确考法 学会解题思路



内角和外角的图解 万图壁纸网




三角形外角和证明方法 百度经验



三角形的内角和推论8 Id拂晓犬吠 博客园



三角形的内角和外角 搜索结果 哔哩哔哩 Bilibili




三角形外角和证明方法 百度经验




三角形内角和定理 平行线的证明ppt课件4下载 牛二ppt



北师大版八年级上册 三角形内角和定理 外角 网易视频
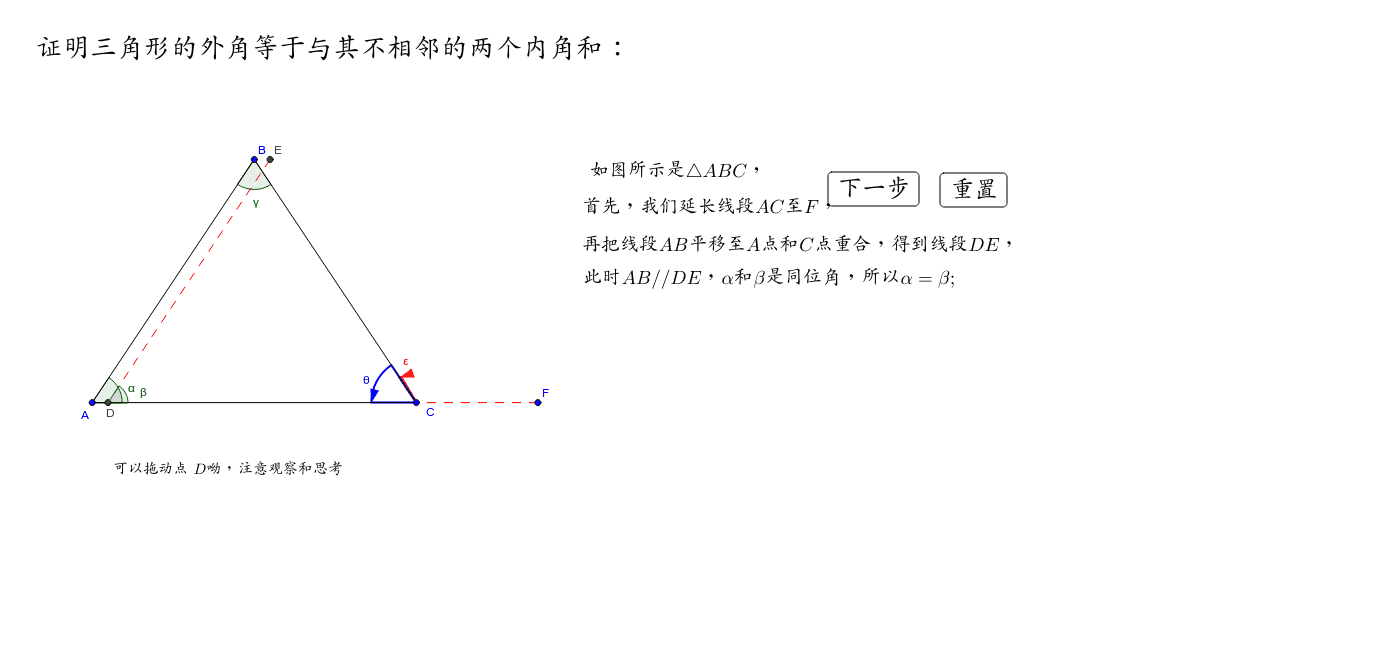



三角形的外角等于与其不相邻的两个内角之和 Geogebra



3分なるほど 三角形の内角 外角の性質について解説 数スタ




外角定理外角定理 Kmbymh



70以上三角形内角外角 シモネタ



三角形的内角和外角 Ppt 第一ppt



1



2 三角形的内角与外角和 Page76 华师大版七年级数学下册电子课本 教材 教科书 好多电子课本网




三角形内角外角定理多边形 三角形png图片素材免费下载 图片编号 Png素材网



三角形内角与外角视频 西瓜视频搜索



14初三数学三角形多边形内角和外角和



47几何原本第一卷命题32 三角形的外交等于与其不相邻的两内角之和 三角形的内角和等于180 哔哩哔哩 つロ干杯 Bilibili


